Lecture Outline
• What we’ve covered so far:
– symmetric encryption
– hash functions
• Where we are heading:
– number theory
– public-key encryption
– digital signatures
• Introduction to number theory
– divisibility
– GCD and Euclidean algorithm
– prime and composite numbers
– Chinese remainder theorem
– Euler Ø function
– Fermat’s theorem
Divisibility
• Divisibility
– given integers a and b, we say that b divides a (denoted by b|a) if b/a
is a whole number (or b = ac for an integer c)
– b is called a divisor of a
• Transitivity theorem
– we are given integers a, b, and c, where all of them > 1
– if a|b and b|c, then a|c
– proof
• Linear combination theorem
– let a, b, c, x, and y be integers > 1
– if a|b and a|c, then a|(bx+cy)
• Proof
– a|b=>
– a|c =>
–
–
• Division algorithm (theorem)
– let a > 0 and b be two integers
– then there exist two unique integers q and r such that 0 ≤ r < a and
b = aq +r
– to show existence:
– uniqueness can be shown by contradiction:
• assume there are integers q' and r' such that b = aq' +r' and
0 ≤ r' < a
• Notation
– the integer q is called the quotient
– the integer r is called the remainder
– [x] is the floor of x (largest integer ≤ x)
– [x] is the ceiling of x (smallest integer ≥ x)
– then q = [b/a] and r = b mod a
Greatest Greatest Divisor
• Greatest common divisor (GCD)
– suppose we are given integers a and b which are not both 0
– their greatest common divisor gcd(a, b) = c is the greatest number
that divides both a and b
– example: gcd(128, 100) = 4
– it is clear that gcd(a, b) = gcd(b, a)
• GCD and multiplication
– we are given integers a, b, and m > 1
– if gcd(a,m) = gcd(b,m) = 1, then gcd(ab,m) = 1
– example: gcd(25, 7) = gcd(3, 7) = 1 => gcd(75, 7) = 1
• GCD and division
– Theorem 1
• we are given integers a and b
• if g = gcd(a, b), then 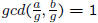
• example: 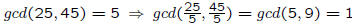
– Theorem 2
• if a is a positive integer and b, q, and r are integers with
b = aq +r, then gcd(b, a) = gcd(a, r)
• we can use this theorem to find GCD
Euclidean Algorithm
• Fact: given integers a > 0, b, q, and r such that b = aq
+r,
gcd(a, b) = gcd(a, r)
• Euclidean algorithm for finding gcd(a, b)
– apply the division algorithm iteratively to compute the remainder
– the last non- zero remainder is the answer
– while a ≠ 0 do
r  b mod a
b mod a
b  a
a
a  r
r
return b
• Example:
– compute GCD of 165 and 285
– steps of Euclidean algorithm:
– the answer is gcd(165, 285) =
Towards Extended Towards Extended Euclidean Algorithm
• Theorem:
– if integers a and b are not both 0, then there are integers x and y so
that ax +by = gcd(a, b)
– we can find x and y using the extended Euclidean algorithm
• Example:
– find x and y such that 285x +165y = gcd(285, 165) = 15
– we start with the next to last equation in our example and work
backwards



