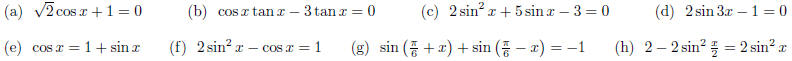Directions: Complete each problem below on
separate sheets, and use this as a cover sheet. Work must be shown to
receive
credit. Specifically, show all relevant steps leading to your solution.
Clearly indicate your final answer. These problems will
be graded for completion and are due at the final exam on Thursday,
May 7. |
1. Solve the following inequalities . Express the solution
set in interval notation.
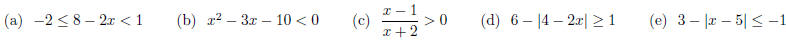
2. (a) Find an equation of the line passing through (-2,
3) and (3,-7).
(b) Find an equation of the line passing though (1, 2) that is perpendicular to
the line in (a).
(c) Is the line y = 2x + 3 parallel to the line in (a)? Why or why not?
3. The manager of a furniture factory finds that it costs $2200 to manufacture
100 chairs in one day and $4800 to produce
300 chairs in one day. Assume there is a linear relationship between cost and
the number of chairs produced.
(a) Find an equation that expresses cost as a function of the number of chairs
produced.
(b) What is the y- intercept of this line , and what does it represent? Hint: It
is a fixed cost.
(c) How many chairs must be produced in one day for the manager to break even?
4. Consider the following piecewise-defined function:
 |
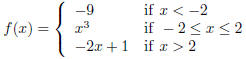(a) Sketch the graph of f , and state its range: |
|
(b) State intervals on which f is increasing, decreasing, or constant: |
5. Find the domain of each function. State your answer in
interval notation where appropriate.
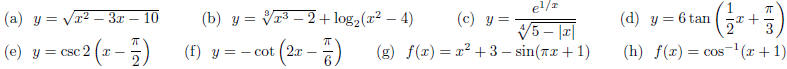
6. Let f(x) = -x2 + x + 1.
(a) Does f have a maximum or minimum value? Why?
(b) Complete the square to find the vertex of f.
(c) Find the average rate of change of f from x = -1 - h to x = -1 (for h > 0).
7. List the transformations applied ( in order ) to the second function below to
obtain f.
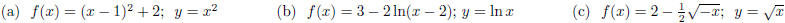
8. A function f is given, and the indicated
transformations are applied to its graph (in the given order). Write the
equation for the final transformed graph. You do not have to sketch the graph of
f.
(a) f(x) = sin-1 x, shift right 4 units, shrink vertically by a
factor of 2, reflect
in the x-axis, and shift down 1 unit.
(b) f(x) = 3x, reflect in the y-axis, stretch vertically by a factor
of 5, reflect
in the x-axis, and shift up 3 units.
9. A gardener has 200 ft of wire fencing. He wants to enclose a rectangular
garden plot adjacent to his house, and then
divide it into seven smaller plots with fencing parallel to one side of the
rectangle, as shown in the figure.
 |
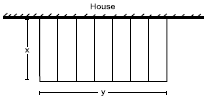(a) Find a function that models the total area of
the seven plots: |
| (b) Find the largest possible total area of the
seven plots: |
10. Express the function in the form f o g.
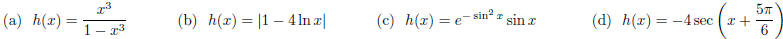
11. Let g(x) = x + 1 and h(x) = 2x2 + 4x - 1. Find a
function f such that f o g = h.
12. For each function f, compute the inverse function f -1.
13. (4 pts) Use long or synthetic division to find the
quotient and remainder.
14. Find a polynomial P with real coefficients which
satisfies the given conditions. If no such polynomial exists, explain
why. You do not need to multiply out your polynomial .
(a) P has degree 7, zeros 2, i, 3 - 5i, and leading coefficient 8.
(b) P has degree 4, zeros -1 (of multiplicity 3) and 1 + i, and constant
coefficient 13.
(c) P has degree 5, zeros 1, 1 - i (multiplicity 2), and leading coefficient -6.
15. Which of the following polynomials exhibit the same end behavior and zeros
as in the graph? Justify your selection(s).
 |
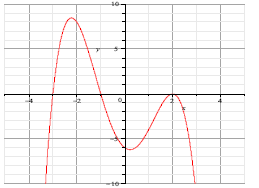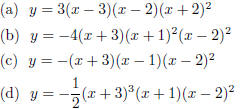
(e) None of the above:
|
16. Find all zeros of the following polynomials. State the
corresponding multiplicities.
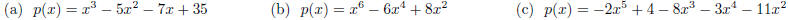
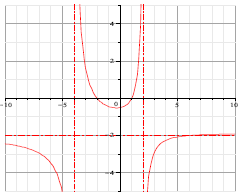
17. Which, if any, of the following rational functions
exhibit the same intercepts and asymptotes as in the graph? Justify
your selection(s).
 |
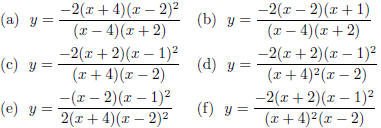
(g) None of the above: |
18. Write an equation representing each graph which has
the given form.
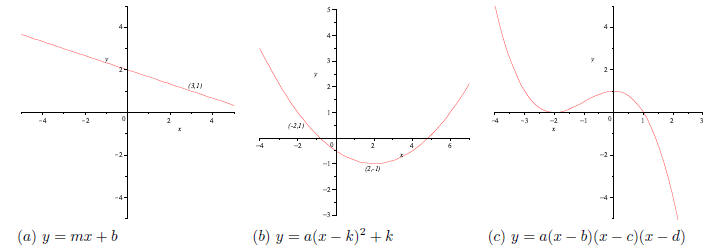
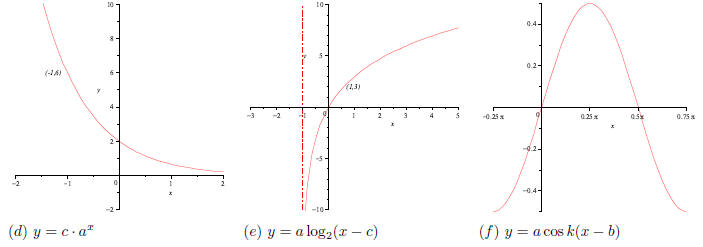
19. Simplify :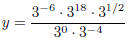 
20. Expand the following logarithmic expressions.
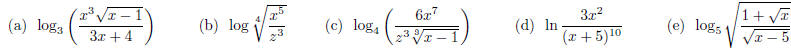
21. Combine the following logarithmic expressions .
Evaluate the resulting logarithm (if possible).
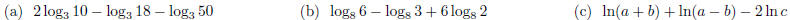
22. Solve the following equations for x.
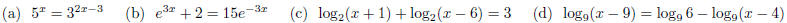
23. A certain type of bacteria thrives when immersed in
water. If a population of 30, 000 of these bacteria are immersed for
30 seconds, their population grows to 120, 000. Assume that the population of
bacteria follows the model: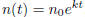 
,
where t is measured in seconds.
(a) Construct a function that models the bacteria population after t seconds of
immersion.
(b) How long must the population be immersed to grow to 240, 000 bacteria?.
24. Find the six trigonometric functions of the following values. Use a
trigonometric identity if necessary.
25. If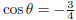 
where µ is in QIII, find the other five trigonometric functions of θ.
26. A man 6-ft tall is standing 5 ft from a lamppost. If the angle of depression
from the lamppost to the tip of his shadow
is 60°, how tall is the lamppost?
27. For each function, find (i) amplitude, (ii) period, (iii) phase shift, (iv)
domain, (v) range, and (vi) vertical asymptotes.
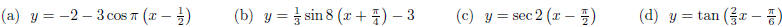
28. Consider all possible triangles ABC which satisfy the
given conditions, and determine the indicated parameter. Use
trigonometric identities if necessary to evaluate associated functions. If no
such triangle exists, explain why.
(a) A = 30°, B = 45°, c = 3, find a
(b) A = 30°, a = 100,
b = 100, find c
(c) a = 9, b = 5,C = 120°, find c
(d) a = 24, b = 15, c = 30, find B
(e) a = 12, b = 6,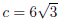 
, find A
(f) C = 30°, b = 22, c = 10, find a
29. To estimate the height of a mountain above a level
plain, the angle of elevation to the top of the mountain is measured
to be 32°. One thousand feet closer to the mountain along the plain, the angle
of elevation to the top is 35°. Find the
exact height of the mountain.
30. A tree on a hillside casts a shadow 50 ft down the hill. If the angle of
inclination of the hillside is 22° to the horizontal
and the angle of elevation of the sun from the tip of the shadow is 52°, find
the height of the tree.
31. A car travels along a straight road heading due east
for 1 hour, then travels for 30 minutes on another road that leads
northeast. If the car has maintained a constant speed of 30 mph, how far is it
from its starting position?
32. Prove the following identities.
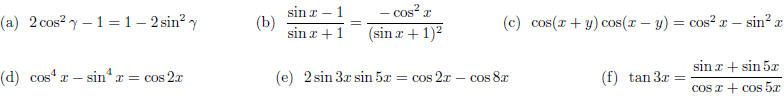
33. Find the exact value of each expression , if it is
defined.
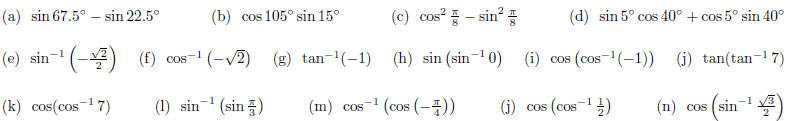
34. Sketch a triangle and/or use an appropriate
trigonometric identity to evaluate the following expressions.
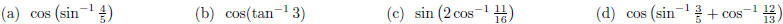
35. Find all solutions of the following equations.
