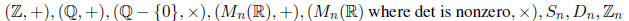Math 109: Outline of the Course

1 Preliminaries

1.1 Set Theory

Definitions Set, element, empty set, cardinality/order, subset/inclusion, containment, power set, intersection,
union, complement

Theorems DeMorgan’s Laws
Know How to Prove Set inclusion, Set Equality
Compute Set operations, cardinality of finite sets, power set

1.2 Functions

Definitions Function, domain, image of a set under a function, injective/one-to-one, surjective/onto, bijective,
composition, inverse, permutation
Know How to Prove Injective, surjective, bijective
Compute Image of a set, composition of functions, composition of permutations, inverses of permutations

1.3 Equivalence Relations

Definitions Equivalence relation, equivalence class, quotient of a set by ~
Know How to Prove Equivalence relation
Compute Equivalence classes, quotients

2 Proofs

Definitions Propositional statement (if p then q), if and only if, converse, negation of a statement, contrapositive
Theorems A propositional statement is true if and only if its contrapositive is true
Know How to Prove If/then statements, if and only if statements, proof by contradiction, proof by contrapositive,
induction
Compute Negation of a statement

3 Number Theory

Definitions Divides, factor, prime, even, odd, gcd, lcm, rational number

Theorems
Division Theorem
* There exist infinitely many primes
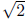* is irrational
Fundamental Theorem of Arithmetic
Compute gcd(a, b) and m and n such that am + bn = gcd(a, b) (Euclidean Algorithm)

4 Metric Spaces

Definitions Metric space, metric, triangle inequality, sup, inf, isometry, open set, neighborhood, closed set,
limit, closure, dense, continuous, Cauchy sequence, complete

Theorems

An open (alt. closed) ball is open (closed)
An arbitrary union of open sets is open
A finite intersection of open sets is open
* An arbitrary intersection of closed sets is closed
* A finite union of closed sets is closed
* If
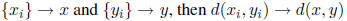
* A sequence can have only one limit (hw)
  f : X -> Y is continuous at x0 if and only if for every
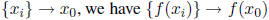
  f : X -> Y is continuous if and only if for every open (alt. closed) set V in Y , 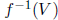is open (closed) in X
* A convergent sequence is Cauchy
R is complete
* A closed subset of a complete metric space is complete

Know How to Prove A set is a metric space, a set is open, a set is closed, a sequence converges to a limit,
a function is continuous, a sequence is Cauchy

Examples
Metric Spaces: Standard metric on Rⁿ, discrete metric
Continuous Functions: polynomials
Complete Metric Spaces: R, any closed set in R

5 Topology

Definitions Topological space, topology, open, closed, neighborhood, continuous, homeomorphism
Know How to Prove A collection of sets is a topology
Examples Any metric space, some other strange ones

6 Group Theory

Definitions Binary operation, closed with respect to *, associative, identity, inverse, commutative, group,
abelian, subgroup, homomorphism, isomorphism

Theorems
* An identity element with respect to * is unique
* If * is associative, inverses are unique
* Then inverse of (a*b) is b⁻¹a⁻¹

Know How to Prove An operation is associative, an element is the identity, an element is an inverse to
another element, an operation is commutative , a map is a homomorphism or isomorphism

Compute Multiplication tables, subgroups, order of elements

Examples