This is a review of the topics you will need from previous
math classes. Note that we expect these
to be skills with which you are already proficient.
This review should help you prepare for the prerequisite test. You can also
refer to this review
throughout the semester. The numbers in parentheses after the topic indicate the
lesson numbers
when you will need this skill as you progress through the course. For example,
you’ll use the skills
reviewed in topic 1 in Lessons 3 and 8.
You will be allowed to use the online calculator on tests. You should become
familiar with it as
soon as possible. It is a bit different from most calculators. If you have
problems, see your
instructor in the Math Lab during his/her office hours. Note: you will not be
allowed to use your
own calculator, only the online calculator. Do not become dependent on a
graphing
calculator!!!
Topic 1: Writing equations of lines (L3, L8)
Given a slope and a point, write an equation of the line.
Example 1: Suppose the slope of a line is -6 and the line passes through the
point (3, -5). Write the
equation of the line.
Use the point-slope form of the equation of the line to solve.
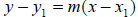
Substitute in the given values:
y - (-5) = -6(x - 3)
Simplify:
y + 5 = -6x +18
Solve for y:
y = -6x +13
Sometimes, you will need to find the slope of the line.
Example 2: Write an equation of the line that passes through the points (-3, 7)
and (4, 12).
Use the slope formula to find the slope of the line:
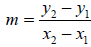
so 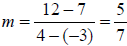
Now proceed as for example 1:
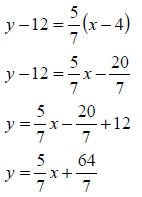
Feel free to use a calculator to help compute with
fractions. Note that the answer is given in
fraction form, so if you use your calculator, you’ll need to be able to convert
back to fractions.
Topic 2: Solving an equation for a given variable (L14, L24)
You should be able to solve an equation for a stated variable, usually y.
Example 3: Solve for y: 2x - 3y = 5
Start by isolating the term containing y by subtracting 2x from both sides of
the equation.
- 3y = -2x + 5
Now divide both sides of the equation by -3 and simplify.
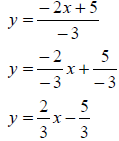
Example 4: Solve for y: xy = -16
To isolate y, you need to divide both sides of the equation by x and simplify.
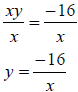
Note that x cannot be 0, since division by 0 is not
defined.
Example 5: Solve for y:
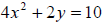
To isolate y, subtract 4x2 from both sides of the equation, then
divide by 2 and simplify.
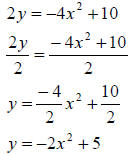
Topic 3: Using interval notation (L10, 11, 12, 13, 14)
You will need to use interval notation extensively throughout the course. The
interval (2, 5) means
all real numbers between 2 and 5, not including either 2 or 5. If you want to
include an endpoint,
you use a bracket instead of a parenthese. So [2, 5) means all real numbers
between 2 and 5,
including 2 but not including 5. The interval [2, 5] includes both endpoints.
You can use interval notation to indicate, say, all real numbers less than 3.
You will write this as
(- ∞, 3). This can also be written as x < 3. You will most likely be asked to
state answers in
interval notation, so you should be able to rewrite the inequality using an
interval.
Example 6: Write using interval notation: x ≥ 6 .
This inequality includes 6 and all real numbers bigger than 6. In interval
notation:
[6, ∞).
Example 7: Write using interval notation: - 3 < x ≤ 12 .
This inequality includes 12, does not include -3 and includes all real numbers
between -3 and 12. In
interval notation:
(- 3, 12].
Topic 4: Solving quadratic inequalities (L10, 11, 12, 13, 14)
Example 8: Solve the inequality: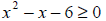
Start by factoring the left hand side of the inequality:
(x - 3)(x + 2) ≥ 0
Next, set each of the binomials on the left hand side equal to zero and solve
each equation for x.
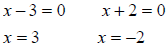
Now draw a number line and use these two values to
subdivide your number line into intervals:
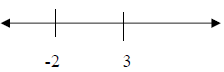
Next, we’ll test each of the three intervals to see if (x
- 3)(x + 2) is positive or negative. We’ll
choose test values in each of the three intervals. Any number in each interval
will do. Convenient
choices for this problem would be -3 (it’s less than -2), 0 (it’s between -2 and
3) and 4 (it’s bigger
than 3).
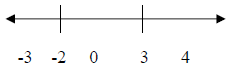
Now try each of the test points in (x - 3)(x + 2).
If x = -3: (- 3 - 3)(- 3 + 2) = (- 6)(-1) = 6
If x = 0: (0 - 3)(0 + 2) = (- 3)(2) = -6
If x = 4: (4 - 3)(4 + 2) = (1)(6) = 6
We’ll record the sign (+/-) of each of these answers in
its interval:
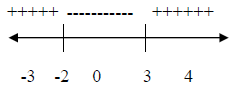
We see from the original problem that we want (x - 3)(x +
2) to be greater than or equal to zero.
From our sign chart, we can see that (x - 3)(x + 2) is positive when x is less
than -2 or greater than
3. Our expression (x - 3)(x + 2) = 0 when x = 3 or -2. Putting this information
together, we have
that (x - 3)(x + 2) ≥ 0 when x ≤ -2 or when x ≥3 . Now write the answer using
interval notation:
(- ∞, - 2]∪[3, ∞).
Topic 5: Finding the domain of a function (L 10, 11, 12, 13, 14)
The domain of a function is the set of all x values that “work” in the
function. We start by assuming
that all real numbers will work, then check to see if we have to exclude any
numbers from the
domain. For example, given the function f (x) = x2 , there are no
trouble spots. Any real number
works in this function. The domain is “all real numbers” which we will write as
(−∞,∞).
The main trouble spots are radical functions , rational functions and logarithmic
functions.
Example 9: Find the domain: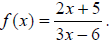
This is a rational function. We have the binomial 3x – 6
in the denominator. Since we cannot let
the denominator be equal to zero, 3x – 6 cannot be equal to zero. So we have:
3x - 6 ≠ 0 which we solve for x to find x≠ 2 .
This tells us that all real numbers except 2 will work. We will write our
answers using interval
notation, so the answer is
(-∞, 2)∪(2, ∞) .
Example 10: Find the domain: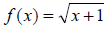
This is a radical function. The quantity under the square
root sign must be non-negative (i.e., either
0 or positive), so we must have
x +1 ≥ 0.
Then x ≥ -1.
In interval notation, [-1, ∞).
Example 11: Find the domain: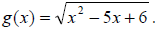
Since we have a square root in the problem, we know that
what is under the square root sign cannot
be negative. So to find the domain, we need to solve the problem,
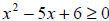 .
.
Factor the left side: (x - 3)(x - 2) ≥ 0 .
The two values at which this inequality equals zero are 3 and 2.
Next, we’ll draw a number line, and split it into three regions, the region from
- ∞ to 2, the region
from 2 to 3 and the region from 3 to ∞:
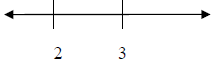
We’ll choose a test value in each of these regions.
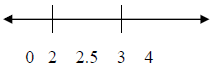
We’ll test these points to determine if the region gives
positive y values or negative y values. To do
this, substitute each test value into (x – 3)(x – 2) and determine if you get a
positive result or a
negative result.
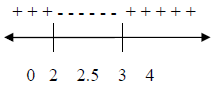
We’ll choose as our answer the intervals which give
positive y values, as well as 2 and 3 which
make the inequality equal to zero:
(-∞, 2]∪[3, ∞) .
Example 12: Find the domain: k(x) = ln(x - 5)
The domain of the function f (x) = ln(x) is (0, ∞). From this, we see that x -
5must be positive.
This is,
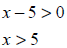
In interval notation, (5, ∞).
Topic 6: Finding information from a graph (L10, 11, 12, 13, 21)
Sometimes you’ll be given the graph of a function. You can read the domain from
the graph. You
can also find the range of the function from the graph, that is, the set of all
y values that “work” in
the function. You’ll also be able to read other information from the graph, such
as the y value
associated with a given x value.
Example 13: Given the graph of f (x), find the domain,
range, f (2), and f (5).
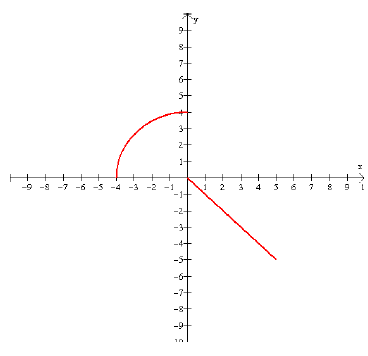
From the graph, we see that there are no x values less
than -4 and there are no x values greater than
5. So the domain is [- 4, 5]. There are no y values below -5 and there are no y
values above 4. So
the range is [- 5, 4]. We can locate f (2) on the graph. Look along the x axis
until you find the
number 2. Then move up or down until your finger is on the graph of the
function. Read off the
corresponding y value. In this case, it’s -2. So f (2) = -2 . Similarly, to find
f (5), move your
finger along the x axis until you find the number 5. Then move up or down until
your finger is on
the graph of the function. Read off the y value. In this case, it’s -5. So f (5)
= -5 .
Topic 7: Multiplying polynomials (Throughout)
Example 14: Simplify: (2x - 5)(3x +1).
Multiply using FOIL (First, Outer, Inner, Last), then combine any like terms.
You are actually
distributing first the 2x and then the -5 to both terms in the second binomial.
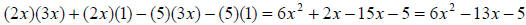
Example 15: Simplify: 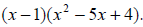
Distribute x to all terms in the second factor, then distribute -1 to all terms
in the second factor.
Then combine any like terms.
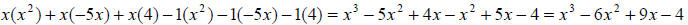
Topic 8: Function notation (Throughout, especially L1,
2, 3, 8, 9, 15)
You should be able to use function notation.
Example 16: Suppose
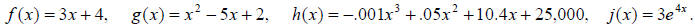
Find 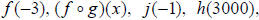 and
and
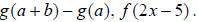
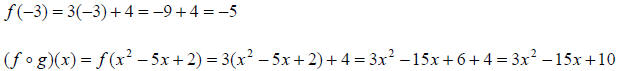
The next two parts of this example will require the use of
a calculator.
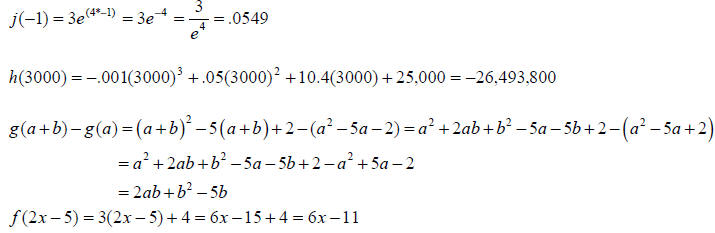
You should also be able to evaluate a variety of problems.
Example 17: Suppose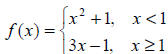 Find f (-3) and f (5) .
Find f (-3) and f (5) .
This is a piecewise defined function. The problem divides
the domain of the function into two
parts, those values less than 1 and those values greater than or equal to 1.
Each part of the domain
is assigned a function. You have to figure out which line applies to the given
value of x, then use
that line to evaluate the function.
First, find f (-3) . Since -3 < 1, we’ll look at the top line.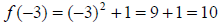
Next, find f (5) . Since 5 > 1, we’ll look at the bottom
line.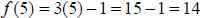
You will not be able to escape word problems in this
class!
Example 18: A study of driving costs based on 1992 model compact cars found that
the average
cost measured in cents per mile is approximated by the function 32.082095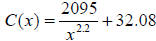 , where x (in
, where x (in
thousands) denotes the number of miles the car is driven in one year. (The
average cost includes car
payments, gas, insurance, maintenance and depreciation.) Find the average cost
of driving a
compact car 25000 in one year.
We are just being asked to evaluate this function at a number, but we must be
careful! The problem
states that x is given in thousands of miles. Since we want to find the cost of
driving 25,000 miles,
we should substitute 25 for x.
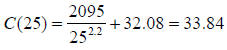 or approximately 34
cents per mile driven.
or approximately 34
cents per mile driven.
Topic 9: Factoring (Throughout, especially L1, 3, 5, 6, 10, 11, 12, 13)
You must (repeat, must!!) be proficient at factoring.
Example 19: Factor: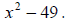
This is the difference of two squares , so it has the factoring pattern
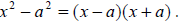
So we have (x - 7)(x + 7) .
Example 20: Factor:
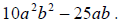
You should always look for a common factor before you try factoring. In this
case, we have a
common factor, 5ab . So we start by factoring that out.
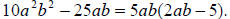
Next we look at the expression inside the parentheses, but it cannot be factored
further.
Example 21: Factor
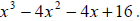
We can factor this by grouping. Group the first two terms together and the last
two terms together.
Then we can factor x2 out of the first two terms and –4 out of the
last two terms:
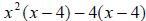
Now our two terms have the binomial (x - 4) in common, so we factor it out:
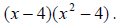
The second binomial can factored some more:
(x - 4)(x - 2)(x + 2)
Example 22: Factor: 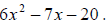
Method 1: Trial and error. 6x2 can have 6x and x as factors or it can
have 3x and 2x as factors.
We’ll start with the factors that are closer together, 3x and 2x. If those don’t
work, we’ll try 6x and
x. Next, the constant -20 has lots of factors, -1 and 20, 1 and -20, -2 and 10,
2 and -10, -4 and 5, 4
and -5. So we’ll try pairs of these factors until we find the one that works. We
check each trial by
multiplying the factors together to see if our factoring gives us what we
started with.
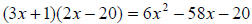 no!
no!
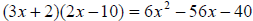 no!
no!
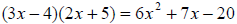 close but no!
close but no!
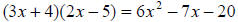 yes!
yes!
There are many other possibilities, but we came across the
right one, so we stopped.
Method 2: Use factoring by grouping.
The trinomial is in the form 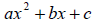 , so find ac .
In our case, it’s (6)(-20) = -120. Next, find
, so find ac .
In our case, it’s (6)(-20) = -120. Next, find
factors of -120 that add up to b, which is -7 in this case. Factors of 120 are 1
and 120, 2 and 60, 3
and 40, 4 and 30, 5 and 24, 6 and 20, 8 and 15 and 10 and 12. Since we have
-120, one or the other
of the factors must be negative (e.g., -10 and 12 or 10 and -12). We need
factors that add up to -7,
so 8 and -15 will do the trick.
Rewrite -7x as 8x – 15x. Then factor by grouping.
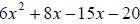
So we have
2x(3x + 4) - 5(3x + 4)
which is
(3x + 4)(2x - 5) .
Method 3: Ms. Leigh’s never-fail method: If you had Leigh Hollyer for Math 1300
or Math 1310,
she teaches another method for factoring which also works. For this problem,
we’ll start by
writing down two factors – we know these won’t work, but this is just our
starting point. We’ll
choose the 6 because it’s the leading coefficient in the problem:
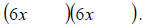
Now find ac. In our case, that’s (6)(-20) = -120. We need
factors of – 120 that add up to our value
for b which is -7. Factors of 120 are 1 and 120, 2 and 60, 3 and 40, 4 and 30, 5
and 24, 6 and 20, 8
and 15 and 10 and 12. Since we have -120, one or the other of the factors must
be negative (e.g., -
10 and 12 or 10 and -12). We need factors that add up to -7, so 8 and -15 will
do the trick.
We can now rewrite our factors:
(6x + 8)(6x -15)
Now get rid of any common factors in the two factors. We can get rid of 2 in the
first set of
parentheses and 3 in the second.
(3x + 4)(2x - 5)
Three methods, same answer.
Example 23: Factor: 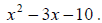
We can use any of the methods shown in example 20, but trial and error is easier
here because the
lead coefficient is 1.
x2 factors into x and x only. We need factors of -10 that add up to
-3. Those are -5 and 2. So we
write our answer:
(x - 5)(x + 2)
Check by multiplying.
Example 24: Factor completely: 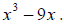
There is a common factor of x, so begin by factoring it out.
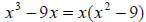
We can factor x2 - 9 , so we continue factoring.
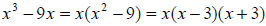
Example 25: Factor completely: 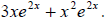
Look for a common factor. This time it includes the exponential function. We can
take out 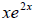 .
.
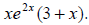
We cannot factor 3 + x any further, so we are done.
Example 26: Factor completely: 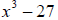 .
.
This is the difference of cubes. There is a factoring pattern:
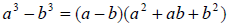 . In our
. In our
case, a = x and b = 3. We have
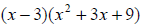 which cannot be
factored any further.
which cannot be
factored any further.
Topic 10: Synthetic Division
You should be able to find a quotient and a remainder using synthetic division.
You should also be
able to tell if a binomial is a factor of the original polynomial.
Synthetic division is an alternative to using long division of polynomials when
you are dividing by
x ± a . You cannot use synthetic division if the power of x is your divisor is
bigger (e.g., x2-5 ).
It easiest to explain synthetic division by example:
Example 27: Use synthetic division to find the quotient and the remainder: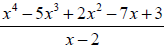
We’ll need to divide by the number that will make x - 2 =
0 , that is 2. To perform the division,
we’ll use only the coefficients of the polynomial.
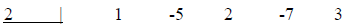
Now, bring down the one. Then multiply by 2 and add what
you get to -5. Write that down. Then
multiply that number by 2 and add what you get to 2. Write that down. Repeat the
process until
you run out of numbers. The last number you get is the remainder. The rest of
the numbers are
coefficients of the quotient, which will be one degree lower than the original
polynomial. So
continuing with our example:
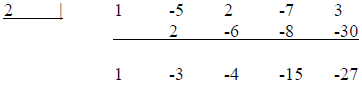
So the quotient is 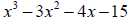 and
the remainder is -27.
and
the remainder is -27.
Example 28: Use synthetic division to find the quotient and the remainder: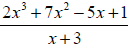
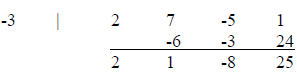
Quotient:
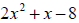 ; Remainder 25
; Remainder 25
Example 29: Use synthetic division to find the quotient and the remainder: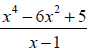
All powers must be accounted for when you set up your
work. In this problem, we have no x3 or x
term in the problem. We’ll put in placeholders (zeros) when we set up the
synthetic division.
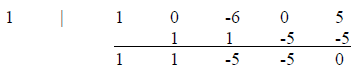
Quotient: 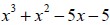 ; Remainder
0. Since the remainder is zero, x – 1 is a factor of
; Remainder
0. Since the remainder is zero, x – 1 is a factor of
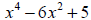 .
.
Topic 11: Using the rules of exponents (Throughout, especially L4, 10, 11,
12, 13, 16)
The definitions and laws of exponents are summarized in Section 9.1 of the
online text. Assume all
variables in these examples are positive.
Following are some examples and frequent student errors:
Example 30: Simplify: - 52
The correct answer is – 25. Note, only the 5 is raised to the second power. The
negative sign is not.
Do not confuse this with (-5)2, which raises -5 to the second power.
Example 31: Simplify: 7x0
The correct answer is 7. Only the x is raised to the zero power, so x0
= 1. Then multiply by 7.
Example 32: Simplify: (7x )0
The correct answer is 1. Anything raised to the zero power is 1. In this case,
7x is raised to the zero
power, so it simplifies to 1. Do not confuse Examples 28 and 29.
Example 33: Write using rational exponents: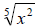
In a rational exponent, the numerator is the power and the
denominator is the root, so in this case,
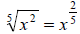
Example 34: Write using a radical: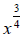
Same as above, so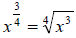
Example 35: Rewrite this expression so that it is not a
fraction: 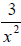 .
.
We can bring the x2 to the numerator by rewriting it as x-2
, so our answer is 3x-2
Example 36: Rewrite this expression so that it does not contain any negative
exponents: x-4 .
We can think of this expression as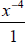 . To
eliminate the negative exponent, we’ll move the x-4 to
. To
eliminate the negative exponent, we’ll move the x-4 to
the denominator and change its sign. So our answer is
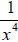 .
.
Example 37: Rewrite this expression so that it is not a fraction: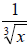 .
.
We can begin by rewriting the denominator using a rational exponent: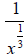 .
.
Now we’ll bring the 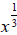 to the numerator by
changing its sign:
to the numerator by
changing its sign: 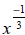 .
.
Topic 12: Simplifying radicals (Throughout)
Example 38: Simplify: 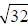 .
.
To simplify this, we will split 32 into two factors, one of which is a perfect
square (i.e., 1, 4, 9, 16,
25, 36, …) In this case, 16 is a factor of 32, so we rewrite 32 as 16 * 2.
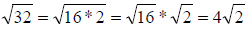
Example 39: Assume x > 0. Simplify:
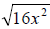
Split the radicand into two factors. Both factors are perfect squares. Take the
square root of each.
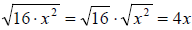
Note, if we had not assumed that x > 0, we’d write the answer as
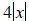 .
.
Topic 13: Exponential functions, logarithmic functions and the number e (L 4,
5, 6, 7, 10, 11,
12, 15)
The number e is the value that the expression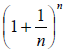 approaches as you let n get bigger and
approaches as you let n get bigger and
bigger. (This idea is called a limit and we will study them this semester.) e ≈
2.718281828... You
will find an ex key on your calculator. (It is exp( ) on the online calculator.)
It is sometimes
convenient to remember that e ≈ 3 .
You should be able to recognize and draw the graph of an exponential function.
Example 40: Sketch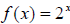 .
.
To sketch this, you can use a table of values, then plot the points . However,
you should be able to
draw a rough sketch from memory.
| x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| f(x) |
1/8 |
1/4 |
1/2 |
1 |
2 |
4 |
8 |
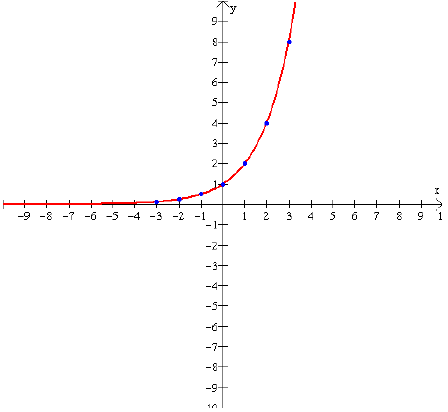
Recall that all basic exponential functions have this same
shape. So any function of the form
f (x) = ax , a > 1, including y = ex , will basically look
like this:
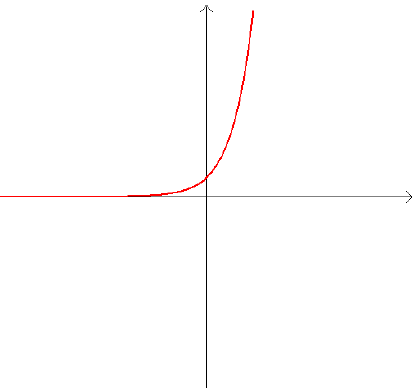
Any function of the form f (x) = ax , 0 < a <
1will be a reflection of the above graph over the y axis:

Some features of exponential functions of the form y = ax
:
Domain is (-∞,∞)
Range is (0,∞)
Graph passes through the point (0, 1)
If a > 1, the function is increasing on (-∞,∞) . If 0 < a < 1, the function is
decreasing on (-∞,∞)
Now we’ll turn our attention to logarithms.
A logarithmic function is the inverse of an exponential function. So if we have
y = 2x , the inverse
of this function is x = 2y . This equation is inconvenient to deal
with. Logarithms help us with this
and allow us to rewrite this equation as 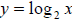 .
Now we can choose values for x, and evaluate
.
Now we can choose values for x, and evaluate
the function to find y. If we choose carefully, we’ll get integers.
The first thing you should be able to do is evaluate a logarithm. You’ll use the
definition of a
logarithm to do this. The definition of a logarithm says that
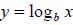 if and only if by = x.
if and only if by = x.
Example 41: Evaluate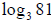 .
.
We can rewrite this as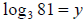 We want to find y.
We want to find y.
Use the definition of a logarithm: 3y = 81
Rewrite the right hand side as 34 . We have 3y = 34
, so y = 4.
Example 42: Graph 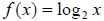
| x |
1/8 |
1/4 |
1/2 |
1 |
2 |
4 |
8 |
| f(x) |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
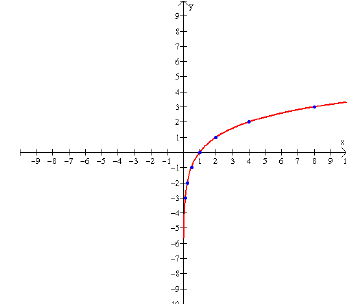
All functions of the form
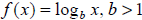 will have the same basic shape.
will have the same basic shape.
All functions of the form 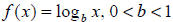 will be the
reflection of the above graph over the x
will be the
reflection of the above graph over the x
axis.
features of basic logarithmic graphs:
Domain is (0,∞)
Range is (−∞,∞)
Graph passes through the point (1, 0)
The function is increasing on (0,∞) if b > 1, and it’s decreasing on (0,∞) if 0
< b < 1.
You will work with the natural logarithmic function most of the time in this
course. This is the
function,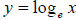 . This function is so important in
mathematics that it has its own notation:
. This function is so important in
mathematics that it has its own notation:
y = ln x.
Log properties are very useful in calculus.
Here are the log properties you need to know:
Suppose M, N and b are positive real numbers, b ≠ 1, and r is any real number.
Then:
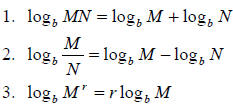
Example 43: Expand using log properties:
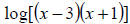
Using property 1, 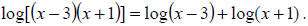 . Note that in this case,
b = 10.
. Note that in this case,
b = 10.
Example 44: Expand using log properties: 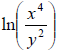
We’ll use properties 2 and 3.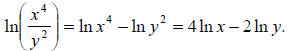
Example 45: Expand using log properties: 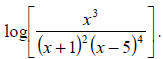
We’ll use all 3 properties.
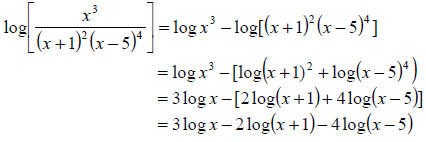
Example 46: Express as a single logarithm: 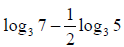
We reverse the process from the previous examples.
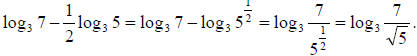
Other properties of logarithms that you need to remember:
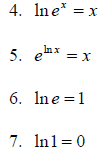
Example 47: Expand and simplify using log properties:
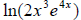 .
.
Using property 1, 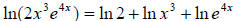
Using property 3, 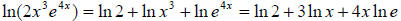
Using property 6, since ln e = 1, we have 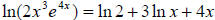 .
.
Topic 14: Solving equations (Throughout, especially L8, 10, 11, 12, 13, 14,
15)
You must be able to solve equations of all types.
Example 48: Solve for x: 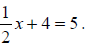
To solve, you must isolate x, so start by subtracting 4 on both sides. Then you
will multiply both
sides by 2.
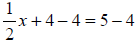
so,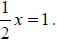
Then 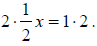
So x = 2 .
Example 49: Solve for x: x2 - 25 = 0
Factor the left side of the equation: (x - 5)(x + 5) = 0 .
Now if ab = 0, then either a = 0 or b = 0, so we have
x - 5 = 0 or x + 5 = 0 , so
x = 5 or x = -5 .
Example 50: Solve for x: 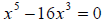
Factor the left side of the equation: 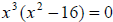 which factors further into
which factors further into 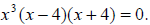
Set each factor equal to zero and solve for x.
x3 = 0 or x - 4 = 0 or x + 4 = 0 , so x = 0, x = 4, or x = -4 .
Example 51: Solve for x: x2 - x -12 = 0 .
Factor the left side of the equation: (x - 4)(x + 3) = 0 , then set each factor
equal to zero and solve
each equation for x to find your answers, x = 4,or x = -3 .
Example 52: Solve for x: 3x2 - 4x - 7 = 3
To begin, we must have one side of the equation as 0. So start by subtracting 3
from both sides.
This gives us 3x2 - 4x -10 = 0 .
We can try to factor this, but it doesn’t factor. In this case, we will use the
quadratic formula,
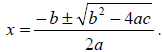 You must know the
quadratic formula!!
You must know the
quadratic formula!!
We have a = 3, b = -4, and c = -10. Substituting these values, we have
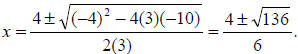 We can simplify the
radical to get
We can simplify the
radical to get
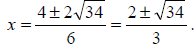 More likely, we will
want to have decimal answers for x, so we will
More likely, we will
want to have decimal answers for x, so we will
compute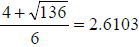 and
and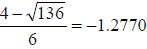
Example 53: Solve for x: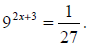
Write both sides of the equation with a base of 3:
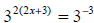
Then 2(2x + 3) = -3.
So 4x + 6 = -3.
Then 4x = -9 , and x = -9 / 4 .
Example 54: Solve for x: 5x= 11
Since we can’t rewrite this using common bases, we must use logarithms. Rewrite
the problem in
logarithmic form:
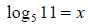
You might need to rewrite this using the change of bases
formula:
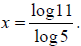
You might see the answer in this form, or it could be
computed using a calculator. In that case,
you’d see
x = 1.4899 .
Example 55: Solve for x: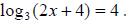
Rewrite in exponential form:
34 = 2x + 4
Solve for x.
81 = 2x + 4
77 = 2x
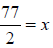
Example 56: Solve for x: 4ln(x -1) = 2
Start by dividing both sides by 4.
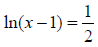
Rewrite in exponential form. Recall that the base of the
natural log is e.
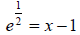
so 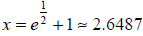
Topic 15: Graphing (Throughout, especially L12, 19, 19,
20, 21)
There are several remaining topics from graphing.
Example 57: Suppose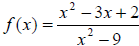 . Find the x
intercept(s), y intercept(s), vertical
. Find the x
intercept(s), y intercept(s), vertical
asymptote(s) and horizontal asymptote(s).
To start, factor everything that is factorable:
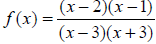
Recall that if you have a common factor in the numerator
and the denominator, you can reduce by
that factor. This will generate a hole in the graph. We don’t have that here.
To find the x intercepts, set f (x) equal to 0 and solve for x.
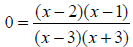
Multiply both sides of the equation by the denominator to
clear the problem of fractions. We have:
(x - 2)(x -1) = 0
So, x - 2 = 0 or x -1 = 0
So x = 2 or x = 1.
We have two x intercepts, 2 and 1.
To find the y intercept, compute f (0) . In this case,
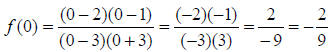
We could also have easily found the y intercept by looking
at the original problem. Sub in 0 for x in
that function, and you can probably find the y intercept in your head.
By the way, we will often ask you to find the y
intercept(s), implying that there can be more than
one. Don’t be fooled. If there are two or more y intercepts for your graph, it’s
not a function.
We’ll only deal with functions in this class.
To find the vertical asymptote(s), set the denominator equal to 0 and solve for
x. Note, if you have
a common factor in the numerator and the denominator (which we don’t have here),
you will reduce
the fraction before finding the vertical asymptote(s).
(x - 3)(x + 3) = 0
So, x - 3 = 0 or x + 3 = 0
And x = 3 or x = -3 . These are the two vertical asymptotes.
Finally, to find the horizontal asymptote, you will need to compare the highest
power of x in the
numerator with the highest power of x in the denominator. This number is called
the degree of the
function. There are three possibilities:
Degree of numerator > Degree of denominator. In this case, there is no
horizontal asymptote.
Degree of numerator < Degree of denominator. In this case, the horizontal
asymptote is 0. We
write this as y = 0.
Degree of numerator = Degree of denominator. In this case,
we make a fraction out of the
coefficients of the terms with the highest power and reduce it to lowest terms.
This is the horizontal
asymptote.
Our problem falls into the third category, since we have x2 in both
the numerator and the
denominator. Both coefficients are 1, so our horizontal asymptote is y = 1.
You should be able to tell by looking at a graph of an equation whether or not
it is a function.
Recall the vertical line test: if a vertical line can cross a graph in more than
one place, the graph is
not the graph of a function.
Example 58: Determine which of these are graphs of functions:
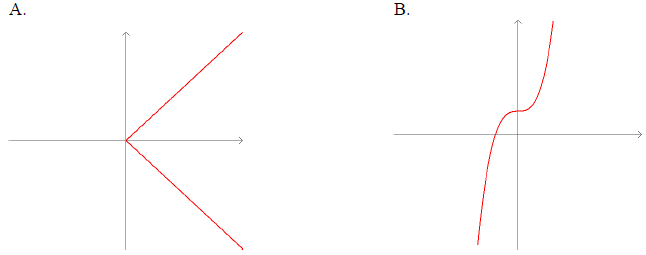
A is not a function. At x = 1, for example, we have two y
values.
B is a function. It passes the vertical line test.
Given a function, you should be able to pick out its graph from a selection of
graphs.
Example 59: What do you know about the graph of the function, f (x) = x3
- 9x ?
1. We know that it is a positive cubic function. Its basic shape is like this:
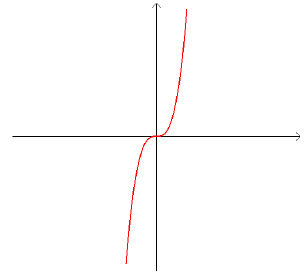
This shows that as x gets bigger, the y values will get
bigger and the graph will be in the first
quadrant. As x moves towards - ∞, (really big, but negative), the y values will
do the same, and the
graph will be in the third quadrant. Recall that cubic functions often have
“humps” in the graph.
You should know the basic shapes of positive quadratic functions, negative
quadratic functions,
positive cubic functions, negative cubic functions, positive quartic (4th
degree) functions and
negative quartic (4th
degree) functions.
2. We can find the zeros (x intercepts) of the function. To do this, we set the
function equal to 0
and solve for x.
0 = x3 - 9x
0 = x(x - 3)(x + 3) (See Example 24 for details on the factoring)
So x = 0, x - 3 = 0, or x + 3 = 0 .
So x = 0, x = 3, or x = -3 are the x intercepts.
3. We can find the y intercept of the function. f (0) = 03 - 9(0) = 0
, so the graph passes through
the origin.
With no more information than this, we can graph the
function. Plot the x and y intercepts. Use the
shape information to fill in the rest.
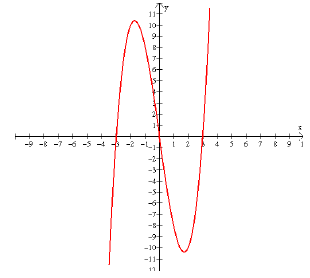
You will not know how high or low the “humps” need to be,
but you can draw a fairly accurate
graph just from this information. Here, we generated a graph, but with the
information we found
you should be able to pick out the correct graph from a selection of graphs.
You should be able to graph certain functions quickly, without a table of values
or looking at a
calculator. Here are some examples.
Example 60: Graph y = 2x + 3.
From this equation, you know that the slope of the line is 2 and the y intercept
is 3. Graph the point
(0, 3) and use the slope o get another point
or two. Connect the dots.
o get another point
or two. Connect the dots.

Example 61: Graph f (x) = x2 .
You should just know this one.
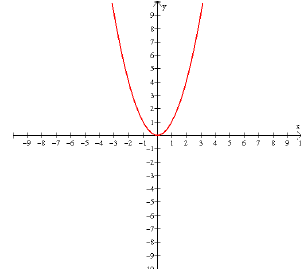
Example 62: Graph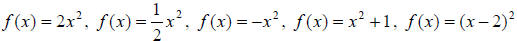
You can use what you have learned about transformations to
graph each of these. The first one is a
bit “narrower”, or closer to the y axis than the problem in Example 60. The
second one is “wider”,
or closer to the x axis than the problem in Example 60. The third one is a
reflection of the function
in Example 60 over the x axis. The fourth one is the graph from Example 60
shifted up one unit.
The last one is the graph from Example 60 shifted two units to the right.
(Recall f (x) = (x + 2)2
would shift to the left.) Here are the graphs:
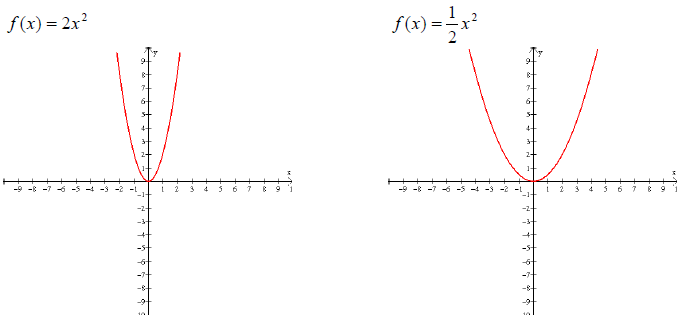
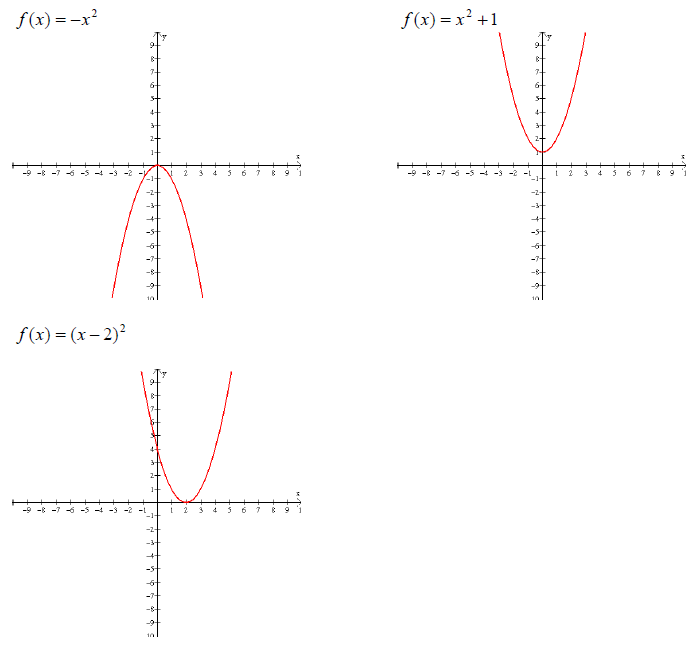
In the next example, we’ll need to look at the graph of a
function and see what we can read from it.
Example 63: What do you know about the equation whose graph is given?
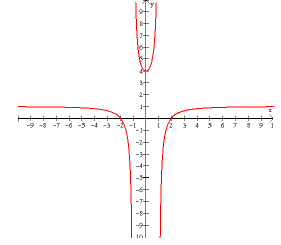
We start by observing that there are two vertical
asymptotes. These must come from the
denominator of the function. The vertical asymptotes are at x = 1 and x = -1, so
we have factors of
(x -1) and (x +1) in the denominator of the rational function.
We have two x intercepts, -2 and 2. This tells us that the function has factors
of (x - 2) and
(x + 2) in the numerator.
We can also see a horizontal asymptote at y = 1. This tells us that the function
has the same highest
power of x in the numerator as it has in the denominator, and that the ratio of
their coefficients is 1,
so they are the same.
We have a y intercept at 4.
So a good guess of the function is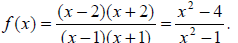 This
function meets all the
This
function meets all the
criteria we noted above.
Topic 16: Solving systems of equations (L24)
Example 64: Solve the system of equations: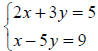
We can solve this by substitution or by
multiplying/adding:
By substitution:
x - 5y = 9 so x = 5y + 9 . Substitute this into the other equation for x and
solve for y:
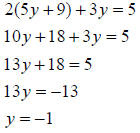
Now that we know what y is, we can find x by substituting
into either one of the original equations.
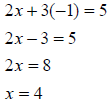
So the solution to the system is the ordered pair (4, -1).
Now we work the same problem, this time by multiplying and adding:
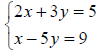
Multiply the bottom equation by -2 to eliminate the x
column,
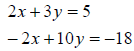
Add the equations:
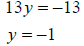
Now that we know what y is, we can find x by substituting
into either one of the original equations.
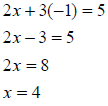
So the solution to the system is the ordered pair (4, -1).
Example 65: Solve the system: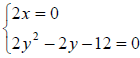
Each equation involves only one variable. Solve each
independent of the other.
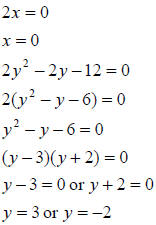
We’ll pair 0 with each of the y values we found. So our
answers are (0, 3) and (0, -2).
Example 66: Solve the system: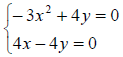
If we just add the two equations together, the y column
drops out. We have
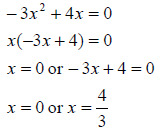
Look at the bottom equation: 4x - 4y = 0
Add 4y to both sides of the equation and divide by 4:
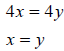
So for our solutions, x = y. Our answers are (0, 0) and 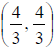
Topic 17: Simplifying expressions (L4, 5, 6, 16)
You’ll need to be able to simplify some algebraic expressions.
Example 67: Simplify: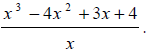
Split up the problem so that each term in the numerator is
divided by the term in the denominator:
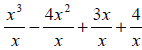
Simplify each term.
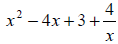
Note: this only works when the single term is in the denominator. You can’t
simplify, for example,
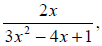 using this method.
using this method.
Example 68: Simplify: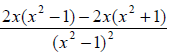
Distribute in the numerator:
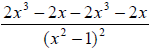
Combine like terms in the numerator
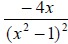
Do not multiply out the denominator.
Example 69: Simplify: 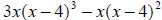
There is a common factor in this problem. Common to the two terms is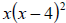 . So we can factor
. So we can factor
this out:
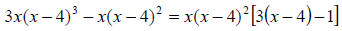
Now simplify inside the brackets:
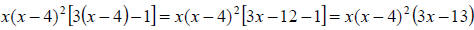
Topic 18: Formulas (L14, 24)
You are expected to remember some simple formulas:
| Perimeter of a square: |
P = 4s , s is the length of a side |
| Perimeter of a rectangle: |
P = 2x + 2y , x and y are length and width,
respectively |
| Circumference of a circle : |
C = 2πr , r is the radius of the circle |
| Area of a square: |
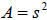 |
| Area of a rectangle: |
A = xy , x is length, y is width |
| Area of a circle: |
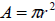 , r is the
radius of the circle , r is the
radius of the circle |
| Volume of a box: |
V = xyh , x is length of base, y is width of the
base, h is
height |
| Volume of a box with a square base: |
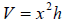 |
| Pythagorean Theorem |
n right triangle ABC, where
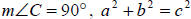 |



