1. Suppose that the augmented matrix for a system of linear equations has
been
reduced by row operations to the given reduced row echelon form. Solve the
system . Assume that the variables are named x1, x2, ..., from left to right.
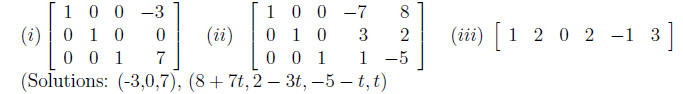
2. Suppose that the augmented matrix for a system of
linear equations has been
reduced by row operations to the given row echelon form. Solve the system by
reducing the matrix to reduced row echelon form. Assume that the variables
are named x1, x2, ..., from left to right.
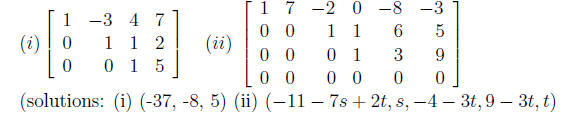
3. Solve the linear system by Gauss- Jordan elimination :
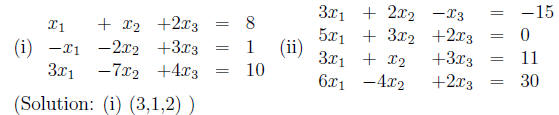
4. Solve the following linear homogeneous system:
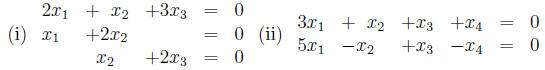
(Solutions: (i) only trivial solution (ii)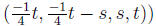
5. Determine the values of a for which the system has no
solutions , exactly one
solution, or infinitely many solutions:
x +2y +3z = 4
3x −y +5z = 2
4x +y −14z = a + 2
(solution: exactly one solution for every a.)
6. What relationship must exist between a, b, and c for
the following linear
system to be consistant?
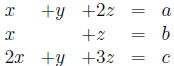
(solution: c = (a + b))
7. Find a cubic polynomial whose graph passes through the
points
(−1, 1), (0, 1), (1, 3) and (4,−1). (solution: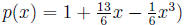
8. Gauss method works by combining the equations in a
system to make new
equations. Can the equation 6x − 9y + 5z = −2 be derived , by a sequence of
Gaussian reduction steps , from the following system?
2x + y − z = 4
6x − 3y + z = 5
(solution: yes; Find the steps!)
9. A box holding pennies, nickels and dimes contains
thirteen coins with a total
value of 83 cents. How many coins of each type are in the box? (3pennies, 4
nickels, 6 dimes)
10. Four positive integers are given. Select any three of
the integers, find their
arithmetic average and add this result to the fourth integer. The numbers
obtained are 29, 23, 21 and 17. What are the integers given. ( Solution: 3, 9,
12 and 21)