1. What is the area of the largest rectangle that can fit
inside a circle of radius 1?
ANS: Area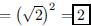 |
2. A rectangle’s length is increased by 20% and its width
is decreased by 20%. How does its area change?
ANS: 1.2L × .8W =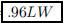 or or
 |
3. Six people are in the same room. If everyone shakes
hands with everyone else in the room, how many
handshakes take place?
ANS: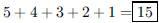 |
4. Two evenly -matched baseball teams, the Green Socks and
the Yellow Elbows, start a 7-game series.
What is the probability that the Green Socks sweep the series in four games?
ANS: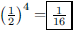 |
5. Sarah averages 50% on multiple choice exams. What is
the probability that she gets at least 2 correct on
a 3-question exam?
ANS: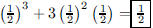 |
6. What fact about the number 1729 did the Indian
mathematician Ramanujan consider interesting?
7. A spider and a fly are at diagonally opposite corners
of a closed cubical box of side length one. What is
the shortest distance the spider can travel to reach the (stationary) fly by
crawling along walls?
ANS: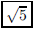 |
8. If the surface area of a cube is equal to 1, what is
its volume?
ANS: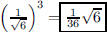 |
9. Out of a group of ten members, in how many different
ways can a president, vice-president, and treasurer
be elected?
ANS: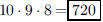 |
10. This 20th century American mathematician introduced
game theory as a mathematical discipline,
conceived the idea of a self-stored computer program, and worked on the
Manhattan project that
developed the atomic bomb. Name this person.
ANS: |
11. What positive number is three times as big as its
reciprocal ?
ANS: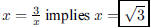 |
12. If the absolute value of x2 + 4 is equal to the
absolute value of 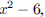 what is x?
what is x?
13. Two wheels are connected by a drive belt. One has a
diameter of 24 centimeters and a speed of 144 rpm.
The other has a speed of 72 rpm. What is its diameter?
ANS:24 × 144 = 72x, Solution is :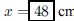 |
14. The vertices of a quadrilateral are at the points (0,
0), (3, 1), (4, 0), and (2,−4). What is the area of the
quadrilateral?
ANS: Area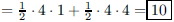 |
15. Find all the integer solutions of the equation
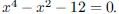
ANS: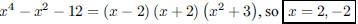 |
16. If a pair of fair dice is rolled, what is the
probability that the sum is 7?
ANS: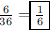 |
17. The base of an isosceles triangle is 4 and the
opposite vertex moves up and down. If the area of the
triangle is plotted as a function of its height, what is the shape of graph?
ANS: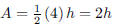 or or
 |
18. What is the distance between two opposite vertices of
a cube of edge 1?
ANS: |
19. If f(x) = 6x − 2, what is f(f(1.5))?
ANS: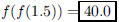 |
20. How many minutes were there in October of 1995?
ANS: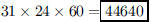 |
21. What famous mathematical object was named after the
mathematician David Hilbert?
ANS: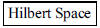 |
22. An octahedron is a regular solid whose 8 faces are
equilateral triangles. What is the distance between a
pair of opposite vertices, assuming each edge of the octahedron is of length 1?
ANS: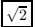 |
23. A shirt has been marked down 20% to $19.20. What was
the original price?
ANS: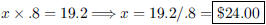 |
24. The 12 faces of a regular dodecahedron are pentagons.
How many edges does a regular dodecahedron
have?
ANS: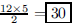 |
25. One fourth of the air in a container is removed by
each cycle of a vacuum pump. What fractional part of
the air remains after 5 cycles?
ANS: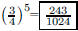 |
26. Three positive integers have a sum of 10. What is the
minimum possible value for the sum of their
squares?
ANS: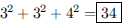 |
27. Find x so that the average of the four numbers 12, x,
30, and 42 is 26.
ANS: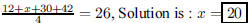 |
28. Find the Greatest Common Divisor of 147 and 77.
ANS: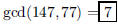 |
29. A wooden cube of edge 4 inches is painted red. The
cube is then cut into 64 one-inch cubes by making 9
saw cuts. How many of the one-inch cubes have exactly 2 red faces?
ANS:12 edges × 2 cubes per edge =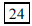 cubes cubes |
30. How many possible ways are there to pick the first
place, second place, and third place in a 10-person
race?
ANS: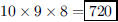 |
31. If f(x) is a linear function with f(2) = 9 and f(4) =
13, then what is f(1)?
ANS: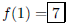 |
32. The first famous woman mathematician was Hypatia, who
lived from 370 to 415 A.D. Although none of
her writings survive, it is believed that her work included integer solutions to
equations. What branch of
mathematics deals with such problems?
ANS: (Source: G. F. Simmons,
Calculus Gems) (Source: G. F. Simmons,
Calculus Gems) |
33. In how many ways can 3 different math books, 2
different stat books, and 1 physics book be arranged on
a shelf, assuming the math books must be together and the stat books must be
together?
ANS: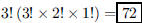 |
34. What is the smallest prime larger than 500?
ANS: nextprime(500) |
35. If a single 60-Watt bulb provides sufficient light to
read a newspaper 5 feet from the bulb, how many
60-Watt bulbs are required in a light fixture 10 feet from the newspaper in
order to provide the same
apparent level of brightness?
ANS: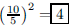 bulb bulb |
36. A wooden cube of edge 4 inches is painted red. The
cube is then cut into 64 one-inch cubes by making 9
saw cuts. How many of the one-inch cubes have exactly 3 red faces?
ANS: 8 corners × 1 cube per corner =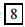 cubes cubes |
37. A quadrilateral kite is made with a right angle at the
top, angles of 2α left and right, and an angle of α at
the bottom. What is α?
ANS: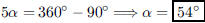 or or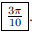 |
38. Find C so that the equation
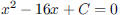 has
exactly one real root.
has
exactly one real root.
ANS: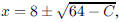 same when same when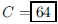 |
39. What is the 10th term of the arithmetic sequence that
begins 49, 43, 37,. . .?
ANS: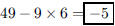 |
40. A shirt has been marked down 20% twice. The current
price is $16. What was the original price?
ANS: (.8) (.8) x = 16, Solution is :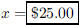 |
41. An equilateral triangle has vertices at (0, 0) and (8,
0). Give one set of possible coordinates for the third
vertex.
ANS: (4, y) where 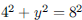 , so vertex at , so vertex at
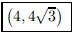 or or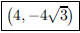 |
42. The 12 faces of a regular dodecahedron are pentagons.
How many vertices does a regular dodecahedron
have?
ANS: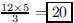 |
43. Express the volume V of a cube as a function of the
area A of one of its faces.
ANS: 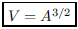 or or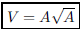 |
44. Two baseball teams, the Green Socks and the Yellow
Elbows, begin a 7-game series. The odds makers
give the green Socks 7 to 5 odds of winning the first game. Assuming the odds
makers are good at their
job, what is the probability that the Green Socks will win the first game?
ANS: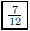 |
45. Sarah averages 50% on multiple choice exams. What is
the probability that she gets exactly 2 correct on
a 3-question exam?
ANS: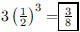 |
46. The 4 faces of a regular tetrahedron are equilateral
triangles. How many edges does a regular tetrahedron
have?
ANS: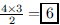 |
47. Kyle uses pure guessing on a TRUE/FALSE exam. Which of
the following options give Kyle the best
chance to score (at least) 80%? (A) A ten-question exam (guess correctly on 8,
9, or 10 questions). (B) A
five-question exam (guess correctly on 4 or 5 questions). (C) The chances are
equal.
ANS: (A) probability of 80% ≈ .054688
 probability of 80% ≈ .188 probability of 80% ≈ .188 |
48. Sarah has a license plate with 2 letters and four
digits, e.g. LW-0508 . What is the probability that at
least one of the four digits is a 7?
ANS: |
49. Express the perimeter P of a square as a function of
its area A.
ANS: |
50. Find a point equidistant from the three points
(−2,−2), (2, 2), and (2,−2).
51. A bag of chicken feed with feed 18 chickens for 72
days. For how many days will it feed 12 chickens?
ANS: (72) 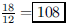 days days |
52. How many primes are there between 90 and 100?
ANS:  (it is 97) (it is 97) |
53. How many different 6-place licence plates are possible
if the first two places are letters and the last 4
places are digits?
ANS: |
54. What Greek philosopher raised paradoxes that argued
that motion is impossible?
ANS:  of Elea of Elea |
55. How many of the 1024 subsets of the set {1, 2, 3, 4,
5, 6, 7, 8, 9, 10} contain the integer 2?
ANS: or or
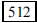 |
56. If f(x) = 2x − 3, what is f(f(f(4)))?
ANS: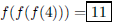 |
57. What is the diameter of a circle with area 25π cm2?
58. A 14-inch pizza is cut into 8 congruent slices. What
is the perimeter of each slice?
ANS:C = 14π so 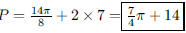 in in |
59. If , what is f(64)?
, what is f(64)?
ANS: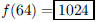 |
60. State the contrapositive of the statement, “If
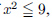 ,
then
,
then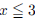 .”
.”
ANS: |
61. Sarah is an 80% free throw shooter. What is her
expected score if she shoots 2 free throws?
ANS: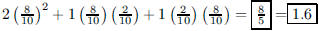 |
62. If 2 cards are drawn from a standard deck of 52 cards,
what is the probability that both are hearts?
ANS: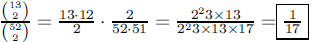 |
63. A triangle has sides of length 13, 10, and 13. Find
the area of the triangle.
Altitude is 12, so Area =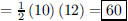 |
64. What is the surface area of a spherical raindrop of
diameter 1 millimeter?
ANS: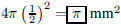 |
65. If 84 centimeters of wire are used to build the
skeleton of edges of a cube, what is the volume of the cube?
ANS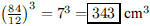 |
66. An elevator moves at constant speed and it takes 12
seconds for an elevator to go from the first floor to
the third floor. How long should it take to go from the first floor to the sixth
floor?
ANS: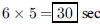 |
67. What is the prime factorization of 999?
ANS: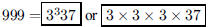 |
68. In how many ways can the U.S. Senate select a
committee of 4 from among its 100 members?
ANS: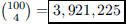 |
69. A wooden cube of edge 4 inches is painted red. The
cube is then cut into 64 one-inch cubes by making 9
saw cuts. How many of the one-inch cubes have no red faces?
ANS: The center of the large cube contains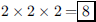 one-inch
cubes one-inch
cubes |
70. The 20 faces of a regular icosahedron are equilateral
triangles. How many edges does a regular
icosahedron have?
ANS: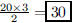 |
71. What mathematician introduced the dy/dx notation in
calculus?
ANS: Gottfried Wilhelm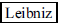 |
72. A biological brick grows 20% in length, 10% in width,
and shrinks in height by 25%. Is its volume larger
or smaller than when it started out?
ANS: (1.2)(1.1)(.75) = .99 |
73. Bo and Jo raise goats and geese. If Bo counts 90 feet
and Jo counts 56 eyes, how many goats and how
many geese do Bo and Jo have?
ANS: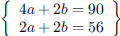 , Solution is: , Solution is: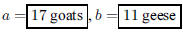 |
74. Name the smallest integer whose square is less than
1000.
ANS: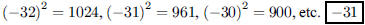 is the smallest is the smallest |
75. Bo scored 67 on the first exam and 75 on the second.
What is the lowest possible score on the third exam
so that Bo’s average for the three exams will be 80?
ANS: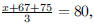 Solution is : Solution is :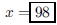 |
76. What number is halfway between 1/6 and 1/8?
ANS: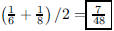 |
77. Expand 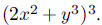
ANS: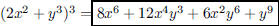 |
78. What cubic curve was named after Maria Agnesi?
ANS: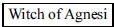 |
79. Six poker players are seated at a round table. How
many rearrangements are possible, if the only
considerations are who is seated at each person’s left, and at each person’s
right?
ANS: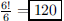 |
80. A Spanish port was protected by large cannons, and
each cannon had a pile of cannon balls nearby
stacked neatly in the shape of a tetrahedron. If each bottom layer contained a
total of 28 cannon balls,
how many cannon balls were there altogether in each pile?
ANS: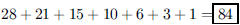 |
81. Write 1995 as a product of primes.
ANS: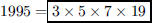 |
82. The Center Ring Janitorial Supply owns a fleet of 3
vehicles: One car, which gets 25 miles per gallon,
and two trucks, each of which gets 10 miles per gallon. If in a typical week the
car is driven 450 miles
and each truck is driven 240 miles, how many miles per gallon is Center Ring’s
fleet getting, rounded to
the nearest mile per gallon?
ANS: mi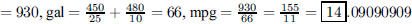 |
83. A pair of dice is rolled. What is the probability that
the sum is either a 3 or a 7?
ANS: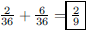 |
84. What is the perimeter of an isosceles triangle with
base 8 and area 12?
ANS: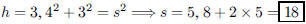 |
85. What are the dimensions of a rectangle with area 110
and perimeter 42?
86. What is the sum of the binomial coefficients (4 choose
zero) plus (4 choose 1) plus (4 choose 2) plus (4
choose 3) plus (4 choose 4)?
ANS: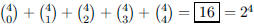 |
87. A gold watch has been reduced by 10%, then by 20%, and
finally sold for $648.00. What was the original
price?
ANS: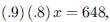 Solution is : Solution is :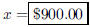 |
88. Every diameter of a spherical orange is 80% fruit and
20% peel. What percentage of the volume is the
peel?
ANS: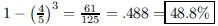 |
89. What is the maximum number of pieces into which a
circular pizza can be cut using 3 chops of a knife
(with no intermediate rearrangements of the pieces)?
ANS: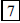 |
90. The 20 faces of a regular icosahedron are equilateral
triangles. How many vertices does a regular
icosahedron have?
ANS: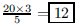 |
91. Factor the polynomial
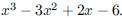
ANS: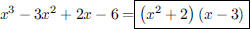 |
92. The 8 faces of a regular octahedron are equilateral
triangles. How many vertices does a regular octahedron
have?
ANS: |
93. What is the perimeter of a right triangle with legs 8
and 15?
ANS: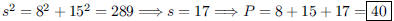 |
94. The sum of two numbers is 14 and their product is 48.
What are the numbers?
ANS: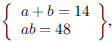 Solution is : Solution is :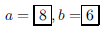 |
95. Give an equation in the form ax + by = c, where a, b,
and c are integers, for the line through the point
(2,−3) and perpendicular to the line 3x − 2y = 4.
ANS: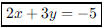 or or
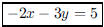 |
96. A pyramid is build out of cubical blocks by placing 64
blocks on the floor, 49 blocks on top of the bottom
layer, and so forth. How many cubes are required to build the pyramid?
ANS: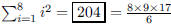 |
97. Find the vertex of the parabola 
ANS: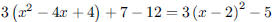 vertex vertex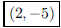 |
98. A bag of Halloween candy contains 6 pieces of
chocolate and 3 pieces of fruit bar. What is the probability
that two items selected at random are both chocolate?
ANS: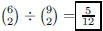 |
99. Sarah is an 80% free throw shooter. What is her
expected score if she shoots a one and one (if she makes
the first she gets a second chance)?
ANS: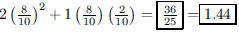 |
100. A ladder leans against a vertical wall. The bottom of
the ladder is 5 feet from the wall and the top of the
ladder is 12 feet above the floor. How long is the ladder?
ANS: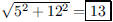 |
101. If 2 is the first prime, what is the tenth prime?
ANS: 2, 3, 5, 7, 11, 13, 17, 19, 23, |
102. A committee of 3 people is to be chosen from among 4
men and 5 women. How many ways can this be
done if the committee must include at least one man and at least one woman?
ANS: |
103. What mathematician first resolved the Königsberg
bridge problem?
ANS: |
104. The compact disk UR2ugly sells at outlet AC for
$13.90 less a discount of 15%, and at outlet DC for
$15.70 less a discount of 25%. Which outlet has the lower price?
ANS: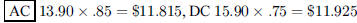 |
105. What is the area of the ellipse 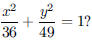
ANS: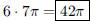 |
106. Factor the polynomial
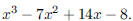
ANS: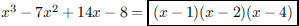 |
107. The sum of two numbers is 13 and their product is 48.
What are the two numbers?
ANS: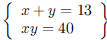 ,Solution is : ,Solution is :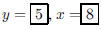 |
108. Give an equation in the form ax + by = c, where a, b,
and c are integers, for the line through the point
(−2, 3) and parallel to the line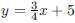
109. What is the area of the triangle bounded by the lines
x = 0, y = x, and 2y + x = 12?
ANS: Vertices (0, 0), (0, 6), (4, 4), base 6, height 4, area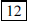 |
110. The height of a rectangle is 25% less than its base.
The perimeter of the rectangle is 64 in. Find the area
of the rectangle
ANS: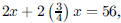 Solution is Solution is in2
in2 |
111. A Social Security number has nine digits. Assuming
the digits are random, what is the expected number
of fives in a social security number?
ANS: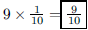 |
112. In which quadrant is the center of the circle
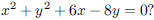
ANS: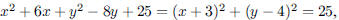 center (−3, 4) center (−3, 4)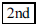 quadrant quadrant |
113. Sarah averages 80% on true/false exams. What is the
probability that she gets exactly two correct on a
three-question true/false exam?
ANS: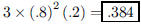 or or
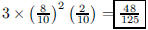 |
114. What is the volume of the tetrahedron whose vertices
are (0, 0, 0), (1, 0, 0), (0, 1, 0), and (0, 0, 1)?
ANS: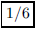 |
115. What is the sum of the roots of the polynomial
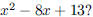
ANS: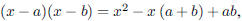 so so
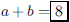 |
116. What is the tenth term of of an arithmetic sequence
whose first term is −5 and whose difference between
successive terms is 3?
ANS: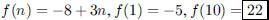 |
117. Solve the equation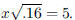
ANS: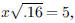 Solution is : Solution is :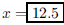 |
118. If
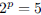 then what is 4p?
then what is 4p?
ANS: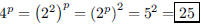 |
119. One of the most influential mathematicians of all
time was the ninth century Arab named Mohammed
ibn-Musa al-Khwarizmi. His last name survives in mathematics today as the term
“algorithm”. His most
important work was Al-jabr wa’l mugab¯alah. What mathematical term was derived
from this title?
ANS: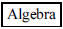 (Source: Boyer and Merzbach,
A History of Mathematics (Source: Boyer and Merzbach,
A History of Mathematics |
120. The average of 5 numbers is 23. What is the average
of these 5 numbers together with 17?
ANS: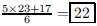 |
121. 200 cadets throw their hats high into the air and
randomly pick up hats afterwards. How many cadets are
expected to pick up their own hats?
ANS: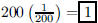 cadet cadet |
122. You decide to guess on a three-question true/false
test. What is the probability that you guess correctly
on exactly 2 of the three questions?
ANS: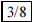 |
123. The average of 5 numbers is 23. The number 3 is
discarded from the collection of 5 numbers. What is the
average of the remaining 4 numbers?
ANS: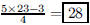 |
124. Neglecting order of addition, in how many ways can 24
be written as a sum of 2 primes?
ANS: 24 = 19 + 5 = 17 + 7 = 13 + 11, |
125. After what mathematician was the Cartesian coordinate
system named?
ANS: (René)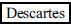 |
126. What is the area of the parallelogram whose four
vertices are at the points (0, 0), (5, 8), (6, 9), and
(11, 17)?
ANS: det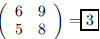 |
127. A regular tetrahedron has edges of length 3. What is
the total surface area of the tetrahedron?
ANS: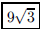 |
128. A circle of radius 1 is divided into 5 pieces. One of
the pieces is 1/2 as large as each of the other four
pieces. What is the area of the smallest piece?
ANS: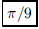 |
129. Six people are in the same room. If everyone shakes
hands with everyone else in the room, how many
handshakes take place?
ANS: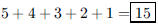 |
130. In which quadrant do the two lines y = 26+2x and y =
6− 3x intersect?
ANS: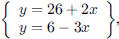 Solution is : Solution is :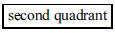 |
131. If a cube has a volume of 343, what is its surface
area?
ANS: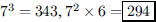 |
132. A car travels 30 miles per hour for 1 mile and 60
miles per hour for 1 mile. What is the average speed of
the car for the 2 miles?
ANS: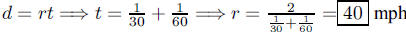 |
133. How far apart are the two points of intersection of
the two curves y = x2 + 1 and y = x + 7?
ANS: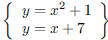 ,Solution is : ,Solution is :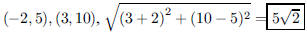 |
134. What is the converse of the statement, “If roses are
red, then violets are blue”?
ANS: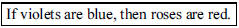 |
135. Bo has $6.00 in quarters and dimes. If Bo has twice
as many quarters as dimes, how many dimes does Bo
have?
ANS: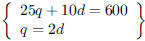 ,Solution is : ,Solution is :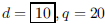 |
136. What is the smallest perfect cube larger than 500?
ANS: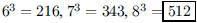 |
137. What is the sum of the roots of the polynomial
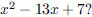
ANS: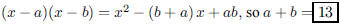 |
138. An automobile is driven 15,000 miles with 5 tires
rotated often for even wear. How many miles are there
on each tire?
ANS: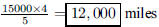 |
139. Out of a group of ten members, in how many different
ways can a president, vice-president, and treasurer
be elected?
ANS: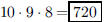 |
140. How many different strings of length 7 can be formed
using the letters in ELLIPSE?
ANS: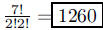 |
141. What is the area of the trapezoid bounded by the
x-axis, the vertical lines x = 1 and x = 3, and the line
y = −3x + 21?
ANS: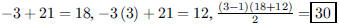 |
142. What is the least common denominator of the two
fractions 1/63 and 1/56 .
ANS: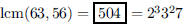 |
143. A computer sequentially computes integers by the
following rule: If n is a square then multiply by 2,
otherwise subtract 2. Starting at n = 13, what is the integer after 6
iterations?
ANS: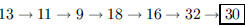 |
144. What is the surface area of a sphere of volume 972π?
ANS: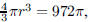 Solution is : Solution is :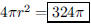 |
145. A solid statue is made by melting 9 cm3 of metal and
pouring it into a mold. A larger model needs to be
constructed by increasing each of its linear dimensions by a factor of 4. How
much metal will the new
statue require?
ANS: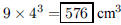 |
146. How many vertices does an n-dimensional cube have?
ANS: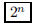 |
147. What is the area of a right triangle having a leg of
length and hypotenuse of length 25?
ANS: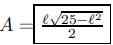 |
148. Bertrand Russell and Alfred North Whitehead wrote the
monumental Principia mathematica. What was
the subject of this publication?
149. What is the greatest integer less than the sum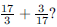
ANS: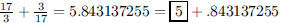 |
150. 200 cadets throw their hats high into the air and
randomly pick up hats afterwards. How many cadets are
expected to pick up their own hats?
ANS: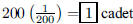 |
151. You currently earn $5.00 per hour delivering pizza.
You are due for a raise, and you figure the probability
of a $.50 raise is 70% and the probability of a $1.00 raise is 30%. What is your
expected new salary?
ANS: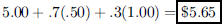 |
152. A square is inscribed in a circle, which in turn is
inscribed in a square. What percentage of the area of the
large square is inside the small square?
ANS: |
153. The probability of picking a dog to finish in the top
3 at the dog track is 1/4 . What is the probability of
picking 2 straight losers?
ANS: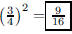 |
154. The polynomial equation
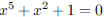 has one real
root. How many imaginary roots does it have?
has one real
root. How many imaginary roots does it have?
ANS: |
155. The number 12 is called abundant because the sum of
the proper divisors 1 + 2 + 3 + 4 + 6 = 16 is
greater than 12. What is the next abundant number?
ANS: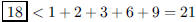 |
156. Andrew Wiles has claimed to have proven something
that had remained an open problem for over 350
years. Either state the problem or name the person who claimed over 350 years
ago to have a solution to
the problem.
| ANS: |
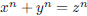 has no positive integer
solutions for n > 2. has no positive integer
solutions for n > 2. |
or
 s Last Theorem s Last Theorem |
157. The diameter of a square of edge a is a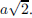 .
The diameter of a cube of edge a is a
.
The diameter of a cube of edge a is a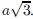 That is
the diameter
That is
the diameter
of a 4-dimensional cube of edge a?
ANS: |
158. What is the perimeter of a regular hexagon inscribed
in a circle of radius 3?
ANS: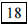 |
159. If it takes two liters of paint to paint a two-meter
model of a battleship, how much paint is required to
paint a three-meter model of the same ship?
ANS: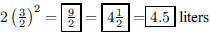 |
160. In the early 1900s a self-taught Indian mathematician
sent some of his unusual mathematical formulas
to the English mathematician G. H. Hardy, who recognized the depth of the
formulas and invited
this mathematician to England. This exceptional Indian mathematician was the
subject of a public
television documentary. A biography, The man Who Knew Infinity, was published in
1991. Name this
mathematician.
ANS: Srinivasa |
161. What is the area of one face of a diamond-shaped kite
whose two sticks are 20 and 26 inches long?
ANS: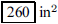 |
162. Three line segments joining the midpoints of the
sides of a triangle determine a smaller triangle whose
sides lie inside the larger triangle. What is the ratio of the area of the
larger triangle to the area of the
smaller triangle?
ANS: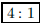 |
163. In how many ways can the U.S. Senate select a
committee of 4 from among its 100 members?
ANS: |
164. Bo is going to the store to buy candy that will cost
somewhere between 5 cents and 26 cents. What is the
fewest number of coins Bo can carry in order to be certain to have exact change
to buy the candy?
ANS: penny, penny, penny, penny, nickel, dime, dime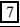 coins coins |
165. The formula 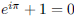 relates five of the most popular numbers in mathematics. What is e rounded to
relates five of the most popular numbers in mathematics. What is e rounded to
6 significant digits?
ANS: e ≈ 2.718281828 ≈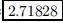 |
166. Three positive integers have a sum of 10. What is the
maximum possible value for the sum of their
squares?
ANS: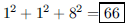 |
167. A contemporary, prolific, Hungarian mathematician is
reputed to have said, “A mathematician is a
machine for converting coffee into theorems.” Name this mathematician.
ANS: Paul |
168. Alice Longwalker plans to walk around the Earth at
the equator. Assuming this is possible (she walks on
water) and that the Earth is a perfect sphere, how much farther will her nose
travel than her feet? Alice
holds her nose 5 feet above the ground when walking.
ANS: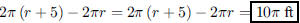 |
169. It is well known that the Hindus introduced zero into
our number system, but that concept was also
developed independently by other civilizations. What Central American
civiliation used a symbol for
zero that resembled a half-open eye?
ANS: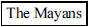 (Source:
Boyer and Merzbach, A History of Mathematics) (Source:
Boyer and Merzbach, A History of Mathematics) |
170. It takes 1000 square tiles to tile a room, or 1440
smaller tiles whose edge is 1 inch less. How large is the
room in square feet?
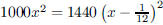 Solution is : Solution is :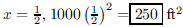 |
171. What is the highest power of 10 dividing 20!?
172. A triangular section of Old Town is divided into a
smaller triangle and two trapezoids by two streets
parallel to one of the boundary streets. The heights of the two trapezoids are
equal to the height of the
small triangle, and the area of the middle trapezoid is 12 acres. How many acres
are there in the larger
trapezoid?
ANS: |
173. A triangle has 3 vertices and 3 edges. A tetrahedron
has 4 vertices and 6 edges. How many vertices and
edges does an n-dimensional tetrahedron have?
ANS: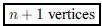 and and 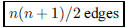 |
174. Solve the system of equations
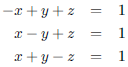
ANS: By symmetry,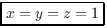 |
175. According to Descartes’ Rule of Signs , how many
positive real roots does the polynomial equation
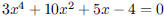 have?
have?
ANS: (since
there is one sign change) (since
there is one sign change) |
176. The plane can be completely tiled using equilateral
triangles, or using squares, or using regular hexagons.
These give the three regular tessellations of the plane. A semi-regular
tessellation is a tiling that uses
at least two different regular polygons, and where every vertex is congruent to
every other vertex. How
many semi-regular tessellations are there?
ANS: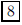 |
177. What is the smallest positive integer with exactly 5
positive divisors?
ANS: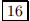 divisors
are {1,2,4,8,16} divisors
are {1,2,4,8,16} |
178. A right triangle has legs of length 6 and 8. What is
the radius of the circle that circumscribes the triangle?
ANS: diameter = 10, radius =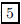 |
179. A pair of dice is rolled 30 times. What is the
expected number of doubles?
ANS: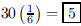 |
180. Twenty students in an algebra class take a
five-question true/false test. None of the students had studied
for the test, so all of them used pure guessing. What is the probability that at
least 10 students score 60%
or higher on the test?
ANS: |
181. Given 5 gallons of a 20% antifreeze/water mixture,
how much pure antifreeze must be added to yield a
50% antifreeze/water mixture?
ANS: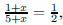 Solution
is : Solution
is : |
182. If g is a function such that g(1) = 2, g(2) = −1, and
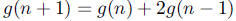
for n ≥ 2, what is g(4)?
ANS: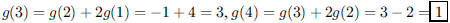 |
183. Write the expression 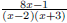 in
the form
in
the form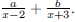
ANS: |
184. A golf bag contains 13 balls, some yellow and the
rest orange. Two balls are drawn at random from the
bag and one is yellow, the other orange. What is the probability that exactly
half of the balls in the bag
are yellow?
ANS: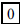 |
185. Two cars start 2 miles a



