MATH DIAGNOSTIC

Note: This is not a test! It will have no effect on your grade. Its sole purpose is to help diagnose
your weakness, if any, in the math , which is needed in this course (not just for the lab).
Your instructor will be happy to help you.

Part 1. Angles and Triangles

1.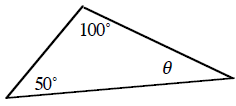	θ = ________________
2.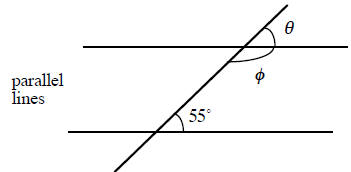	ø = _________  θ= ________
3.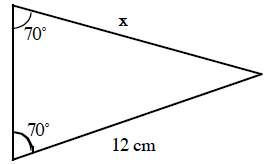	x = _________________
4.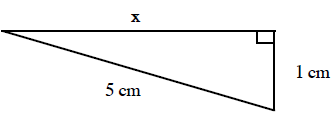	x = _________________

Part 2. Trigonometry

5.

 

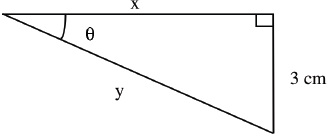
sin θ = 0.60

x = ______________

y = ______________

6. If sin 35° = cos θ, then θ = _____________

7. If sin θ = 0.80, then cos θ = _____________ and tan θ = _____________

8.

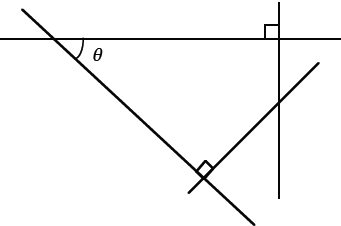
Mark all angles that are equal to the angle θ .
How many did you mark (including the one
that was already marked)? _____________

9. For what values of θ, if any, is the following expression true ?
sin² θ + cos² θ = 2.0
θ = ____________________________

Part 3. Scientific Notation

In scientific work, it is convenient to express numbers as the product of a number between 1
and 10 multiplied by an appropriate power of 10. Thus 0.00050 becomes 5.0*10^-4, and 1,800,000
is written as 1.8*10⁶. This way of writing numbers is called scientific (or powers of ten) notation.
Carry out the operations indicated and express the results in scientific notation.

10. 2 * 0.000015 = _________________________________

11. (0.00002)³ = ______________________________

12. (7.1 * 10⁵) + (2.2 * 10⁴) = _______________________________

13. (4*10⁸) * (9*10⁹) = _______________________

14. (3*10⁷) * (6*10^-12) = ________________________

Part 4. Algebra

15. Given that 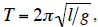write an expression, which contains only l on the left-hand side.
l = ___________________

16. 3x - 5 = 13 x = __________________

17. a² + a² + 2a² = _________________

18. The radius of a circle is R . Write an expression for the area of the circle. ______________
Write an expression for the circumference of the circle. ______________________

19. The radius of a cylinder is R and its height is h.
Write an expression for the volume of the cylinder. _________________________

Part 5. The Straight Line Graph

If the relation between x and y is given by: y = mx + b ,
then it may be pictured by a straight line on the y (vertical axis) versus x (horizontal axis) graph.
The parameter b, called the y-intercept, represents the value of y for x = 0. The parameter m is
equal to the slope of the straight line and is also equal to the tangent of the angle that the line makes
with the x-axis.

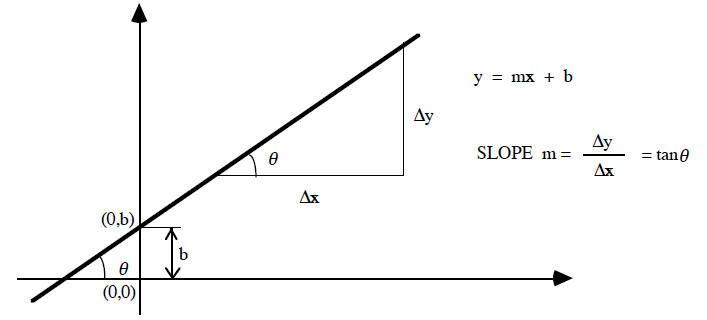
Sometimes it is not possible to read the value of b directly from the graph. In that case, b
has to be calculated. First, find the slope m and then select any point on the straight line and read x
and y values for that point. Substituting m , x, and y into the straight-line equation, you will be able
to calculate the value of the y- intercept b (b = y - mx).

20. From the graph below , find the slope m and the y-intercept b.

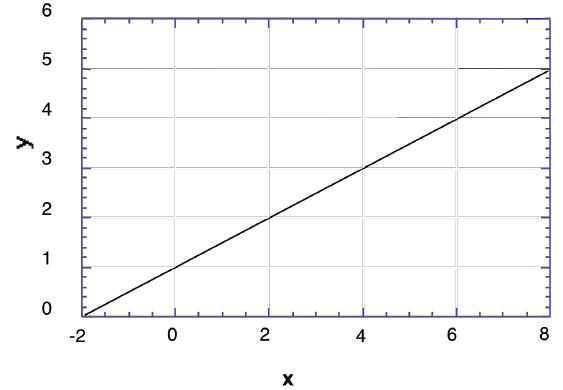
m = ____________________ b = _____________________

21. From the graph below , find the slope m and the y- intercept b .

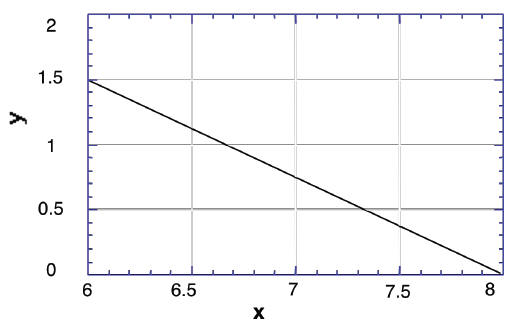
m = ____________________ b = _____________________