Midterm I Information

WHEN: Monday, March 9, in class (no notes or books)

COVERAGE: The midterm will cover the material discussed in lecture from Sections 1.1-1.6,
2.1-2.4, 3.1-3.2.

Note, you are only responsible for material that we explicitly discussed in lecture from the sections
above. Consult your class notes on this. For instance, we didn’t cover Riemann Surfaces (subsection
2.4.1), nor the notion of similarity mappings in Section 2.1.

EXTRA OFFICE HOURS:

Thursday, March 5, 4-6 p.m. and 8-10 p.m.
Friday, March 6, 9-10 a.m. and 11-1 p.m.
Sunday, March 8, 2-5 p.m. and 7-11 p.m.
Monday, March 9, 8-9:30 a.m.

REVIEW SESSION:

Saturday, March 7, 3-5 p.m. (MH-416)

STUDYING: Here is an overview of the topics we have covered. You should be comfortable with
all of the following words below:

Chapter 1: Complex Numbers: Real part , Imaginary part, Conjugate, Modulus, Argument, Field
axioms. Real axis, imaginary axis. Triangle inequality . Forms of a complex number: cartesian, polar,
exponential. Euler’s Formula. Fundamental Theorem of Algebra . nth roots of unity. Quadratic
formula. Topology: curve, initial point, terminal point , closed curve, simple curve, positive orientation,
-neighborhood, open disk, closed disk, punctured disk, interior point, exterior point, boundary
point, accumulation point, open set, closed set, connected set, bounded set, region, closed region,
domain, Jordan curve theorem .

Chapter 2: Complex- valued function : domain, range/image, Cartesian representation, Polar representation.
One-to-one and onto: inverse function. Linear transformation : translations, rotations,
magnifications. Power and root functions: principal nth root function. Limit of a function. Continuous
function at z₀. Combinations of continuous functions remain continuous. Branch of a function,
branch cut, branch point.

Chapter 3: Differentiable function at z₀. Analytic function at z₀. Entire function. Singular points
of a function. Differentiation rules: power rule, sum/ difference rules , product rule , quotient rule,
chain rule. L’Hopital’s Rule. Cauchy- Riemann equations : cartesian and polar forms.

IMPORTANT THEOREMS:

• Theorem 1.1: Basic properties of complex numbers
• Theorem 1.2: Triangle Inequality
• Theorem 1.4: (Corollary to) Fundamental Theorem of Algebra
• Theorem 1.5: Quadratic Formula
• Theorem 1.6: Jordan Curve Theorem
• Theorem 2.1: Limits of functions in Cartesian form
• Theorem 2.2: Limits respect addition, subtraction , multiplication, and division
• Theorem 2.3: Continuous functions in Cartesian form
• Theorem 2.4: Continuous functions are preserved by addition , subtraction, multiplication, division, composition
• Theorem 3.1: Differentiable functions are continuous
• Theorem 3.2: L’Hopital’s Rule
• Theorems 3.3 and 3.4: Cauchy-Riemann conditions for differentiability
• Theorem 3.5: Polar form of Cauchy-Riemann equations
• Theorem 3.6: Analytic functions of constant modulus are constant
• Theorem 3.7: Analytic functions of derivative zero are constant

THINGS TO BE ABLE TO DO:

• Given z₀ ∈C, be able to compute 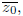Re(z₀), Im(z₀), |z₀|, arg(z₀), Arg(z₀).
• Be able to prove basic properties involving conjugate, modulus, real/imaginary parts, etc., such as in Theorem 1.1.
• Be able to apply the Fundamental Theorem of Algebra.
• Be able to locate complex numbers geometrically in the plane. Same thing for a subset of the complex plane.
• Be able to convert to and from Cartesian , polar, and exponential representations of a complex number.
• Be able to perform arithmetic operations on complex numbers: addition, subtraction, multiplication, division, powers, and roots.
• Be able to prove facts about arg(z), such as Theorem 1.3.
• Be able to apply the Quadratic Formula to find roots of any quadratic equation, including those with non-real coefficients.
• Be able to parametrize a curve in the complex plane.
• Given a subset S of C, be able to decide (with proof) if S is open, closed, connected, bounded, a domain, a region, etc.
• Given a subset S of C, be able to find its accumulation points, its boundary points, its interior
points, and its exterior points.
• Be able to write a function w = f(z) in Cartesian form and in polar form.
• Be able to decide if a function f : C -> C is one-to-one, onto, both, or neither. In the case
of “both”, be able to write the inverse function. In the case when f is not onto, be able to
compute the image of f.
• Be completely comfortable with linear transformations (translations, rotations, magnifications,
and compositions thereof).
• Be familiar with w = f(z) = zⁿ and w = g(z) = z^1/n. Are they bijective? If not, how can
we make them so? With the nth root function g, understand its many branches, branch cuts,
branch points, and the principal one.
• Be able to prove or disprove existence of limits, and compute their value when they do exist.
The former situation may requir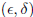e -argument or could appeal to known continuity of the
function involved. The latter situation requires consideration of 2+ paths approaching the
limit point that result in different answers.
• Be able to decide if a given function f is continuous at a given point z₀ or on a given domain.
• Be able to apply Theorems 2.1-2.4 to address limits and continuity. Examples 2.18 and 2.19
are also relevant.
• Be able to decide (with proof) if a given function f is differentiable at a given point, analytic
at a given point.
• Be able to decide if a given function f is entire. If not, be able to find its singular points.
• Know all rules for differentiation (Equations 3.4 - 3.12) and be prepared to prove them or
apply them.
• Be able to use L’Hopital’s Rule to facilitate the evaluation of limits.
• Know the Cauchy-Riemann equations, and be able to use them to determine differentiability
of a given function f.
• Understand Theorems 3.6, 3.7, and their proofs. Applications (such as Problems 12 and 15 in
Section 3.2) abound.

ADVICE: I suggest reviewing the group works, the quizzes, and the weekly practice quizzes carefully.
If you have time, it might be best to try re-working those exercises from scratch and looking
up the answers afterwards. You will not have time to re-do all of the homework, but you might try
some of them again, especially the ones that will assist you with the “THINGS TO BE ABLE TO
DO” listed above. Try to re-do problems from scratch, rather than just looking up solutions that
I’ve posted. General rule of thumb: The more time we spent on a topic or type of problem, the
more likely it is to appear in some form on the exam.

It may also help you to discuss solutions to problems with other people. Explaining yourself to
someone else can be a tremendous benefit to both of you, especially with this particular material.
Often, there is more than one way to look at things, so it is useful to hear each other’s perspective
on the problems at hand.

Finally, you can ask me questions as much as you want, and I will be happy to review or pop-quiz
a topic with you if you feel shaky. Basically, I’m here to help and I want everybody to do well, so
please don’t be shy :=) !!

Once you have feel you have studied sufficiently and feel fairly confident, try the sample midterm I
have posted on the webpage.