1 Definitions and a positive result
For a brief history of the problem of how to identify a complete matrix ring,
and of how to present a matrix ring by generators and relations, we refer to
the introduction of [1]. In that paper it was established that a k- algebra R
is an (m+n) ×(m+n) matrix algebra if and only if there are three elements
a, b, c ∈ R satisfying the relations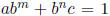 
and 
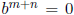. There it
was also shown that the k-algebra presented by the two generators a and b
and (1) below is nonzero if i/m = j/n. This paper deals further with these
two-element presentations (1), whose theory is by no means as complete as
that of the three-element presentation studied in [1].
Unless otherwise stated k is an arbitrary associative commutative ring with
1. All algebras will here be assumed associative and with 1.
Let us make
Definition 1.1 Let i, j, m and n be positive integers. Let R(k; i, j, m,
n)
denote the k-algebra presented by two generators a and b and the relations
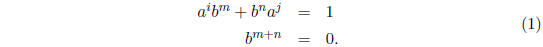
We will show that the question whether R(k; i, j, m, n) is nonzero, and
whether it admits a homomorphism to a matrix algebra over k, will only
depend on the ordered pair of positive rational numbers (p, q) = (i/j, m/n).
For a field k we will show that R(k; i, j, m, n) can be mapped into
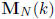
for some N and hence is nonzero if p is arbitrary and q = 1. On the other
hand in the next section we will show that for all k, R(k; i, j, m, n) is
trivial
if q ≠ 1 and p = 1.
We will begin with the following lemma which will be useful in proving the
next theorem.
Lemma 1.2 Let R be a ring, and d a positive integer, and regard R as
embedded in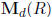 
by the diagonal embedding. Then
every element of R
has a d-th root in .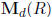
Proof: A d-th root of x is given by
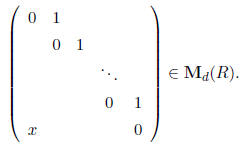
We can now show that the behavior of R(k; i, j, m, n) only depends on the
ordered pair (i/j, m/n).
Theorem 1.3 For positive integers c and d we have
the following:
1. R(k; i, j, m, n) is nonzero if and only if R(k; ci, cj, dm, dn) is nonzero.
2. R(k; i, j, m, n) can be mapped into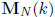 
for
some positive integer N,
if and only if R(k; ci, cj, dm, dn) can be mapped into
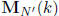for some
N'.
Proof: Let c and d be positive integers. It is clear that if R(k; ci, cj, dm, dn)
is nonzero then so is R(k; i, j, m, n), also if R(k; ci, cj, dm, dn) can be
mapped
into 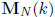for some N then so can R(k; i, j, m, n).
Assume R(k; i, j, m, n) to be nonzero. If we let e be a common multiple
of c and d, then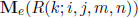 
is a nonzero k-algebra in which
the relations defining R(k; ei, ej, em, en) have a solution by Lemma 1.2.
R(k; ei, ej, em, en) is therefore nonzero and hence also R(k; ci, cj, dm, dn).
Let us finally assume that R(k, i, j, m, n) can be mapped into
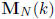for
some N. Equivalently there are matrices a and b in
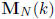satisfying (1).
Let again e be a common multiple of c and d . Then by Lemma 1.2 we
can find e-th roots of a and b in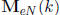 
. Hence R(k; ei, ej, em, en) can be
mapped into 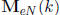, and therefore so can R(k; ci,
cj, dm, dn).
Definition 1.4 Let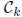 
be the set of
ordered pairs of positive rational numbers
(i/j, m/n) such that R(k; i, j, m, n) is nonzero, and let
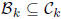be the
set of (i/j, m/n) such that R(k; i, j, m, n) can be mapped into
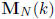for
some positive integer N.
Theorem 1.3 shows that the sets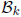 
and
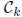are indeed well
defined.
There are some basic relations worth noticing. We see by left-right symmetry
that for X ∈ { B, C} we have
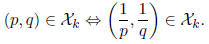
If there exists a homomorphism of commutative rings k → k'
then
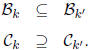
If k and k' contain fields of the same characteristic,
then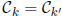 
.
We will prove the next theorem in a few steps .
Theorem 1.5 If k is a field and p a positive rational number then (p, 1) ∈
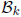
Let us first notice a few things that will ease the task. When seeking a map
R(k; i, j, 1, 1) →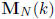
for some N it suffices by Theorem 1.3 to consider
the case gcd(i, j) = 1.
Lemma 1.6 If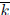 
is the algebraic closure
of the field k, then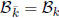 
.
Proof: Clearly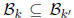 
if k is a sub field of k'. If k'/k is a
finite field
extension then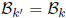 
. Since
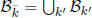where the union is taken over
all finite field extensions k'/k, the lemma follows.
Theorem 1.5 will clearly follow once we have proved the following lemma:
Lemma 1.7 If k is an algebraically closed field and i, j are relatively prime
positive integers then one can always find a nonzero k-algebra homomorphism
R(k; i, j, 1, 1) →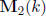 
.
Proof: We will consider the following three cases:
Case 1. i + j is even (hence i, j are odd): Here we clearly have a surjection
R(k; i, j, 1, 1) → 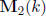given by
.
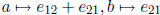Case 2. char(k)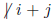 
: By left-right symmetry of R(k; i, j, 1, 1) we may
assume j > i to hold. Consider the polynomials
.
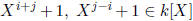Since char(k) does not divide i + j we have that
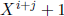is separable and
has therefore a root which is not a root of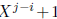 
.
Hence in this case there
is an r ∈ k such that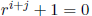 
and
.
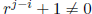Now for this r ∈ k the k-algebra homomorphism R(k; i, j, 1, 1) →
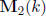
given by
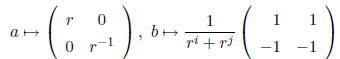
is clearly well defined.
Case 3. char(k) l i+j and i+j is odd: Let char(k) = p. Since gcd(i, j) = 1,
we have gcd(i, p) = 1 and thus, i is invertible in the prime field of k with an
inverse c. Consider the k-algebra homomorphism R(k; i, j, 1, 1) →
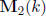
defined as follows:
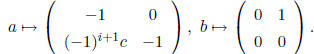
We easily see that:
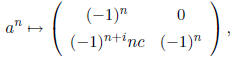
and computation using the fact that i+j is odd shows that
we get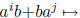 
1 an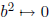d 
. Hence the above homomorphism is well
defined.
