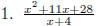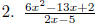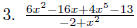5.1 Addition and Subtraction of Polynomials
Definition 1. A polynomial is a finite sum of terms in which all
variables have whole number
exponents (recall whole numbers are positive and include 0) and no variable
appears in the denom-
inator.
EX 1. -
1. The following are not polynomials. State why not:
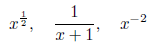
2. Here are a couple examples of polynomials:
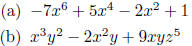
Recall that the degree of a term is the sum of the
exponents of the variables. The leading
term of a polynomial is the term of highest degree and the leading
coefficient is the coefficient of
the leading term.
EX 2. For the polynomial -7x6 + 5x4 - 2x2 + 1 we have:
|
Degree of the polynomial |
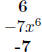 |
|
Leading Term: |
|
Leading Coefficient: |
Classifying Polynomials
We can classify polynomials in a couple of ways. First by the number of terms:
| Terminology |
Number of terms |
Examples |
| Monomial |
one term |
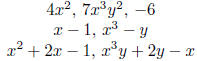 |
| Binomial |
two terms |
| Trinomial |
three terms |
We can also categorize polynomials by the degree of the
polynomials
•
Linear polynomial - polynomial of degree 0 or 1.
•
Quadratic Polynomial - polynomial of degree 2.
•
Cubic Polynomial - polynomial of degree 3.
After degree three we usually just refer to the polynomial as n-th degree, ie
4th degree, 5th degree,
etc.
We generally will write polynomials in descending order in terms of degree .
EX 3. For example we would write x + 6x2 + 2x3 - 1 as
2x3 + 6x2 + x - 1
Where we start with the highest degree term and continue in descending order.
5.1.1 Polynomial Functions
Polynomials can also be written as function (using function notation).
EX 4. The following are polynomial functions.
• f(x) = x2 + 3x + 2
• P(x) = 2x3 - 3x2 + x - 7
When written as a function, we can graph polynomials.
EX 5. -
1. Graph y = x2
The graph we get is called a parabola. All quadratic
polynomials have parabolas as graphs.
In this case the parabola opens upwards. Whenever the leading coefficient is
positive the
parabola opens upwards.
2. Graph y = -x2

We notice that we now have a negative leading coefficient
and the parabola opens downwards.
5.1.2 Add and Subtract Polynomials
To add or subtract polynomials we just combine like terms
EX 6. Simplify the following:
1. Add (3x2 - 2x + 7) + (2x2 + x - 3)
2. Add (2x2y - 4xy + 7) + (3x2y + 5xy - 2y - 8)
3. Subtract (-x2 + 5x - 13) from (x3 - 2x + 9)
4. Simplify 8x2y - 7xy2 + 1 - (x2y - 2xy2 + 6y)
5.2 Multiplication of Polynomials
We learn how to multiply polynomials in steps .
5.2.1 Multiply a Polynomial by a Monomial
To begin we recall product rule for exponents
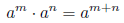
EX 7. Monomial Monomial: Multiply
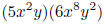
In order to do more complicated products we need to recall
the distributive property
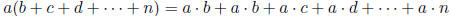
EX 8. Multiply: 3x2y(2xy + 7xy2 - 8)
5.2.2 Multiply a Binomial by a Binomial
Abstractly we multiply binomial times a binomial as follows:
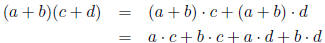
However we will generally use the FOIL method. FOIL stands
for: Let's look at
Let's look at
some examples
EX 9. Multiply:
1. (4x - 3)(x + 2)
2. (3x2 + 4)(2x - 5)
5.2.3 Multiply a Polynomial by a Polynomial
Let's look at a couple examples.
EX 10. Multiply:
1. Multiply x2 + 2 - 3x by 4x2 - 1
2. Multiply 2x2 + 5xy - 4y2 by x + 3y
5.2.4 Some Formulas and Special Cases
The following situations come up often enough that we look at them seperately:
(a + b)2 = (a + b)(a + b) = a2 + 2ab + b2
(a - b)2 = (a - b)(a - b) = a2 - 2ab + b2
and
(a + b)(a - b) = a2 - b2
EX 11. Multiply:
1. (x + 2)2 (warning: (x + 2)2 ≠ x2 + 4)
2. (3x2 - 7y)2
3. [x + (y - 3)]2
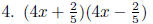
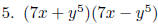
5.3 Division of Polynomials
5.3.1 Division by Monomials
Recall the following properties that we will use:
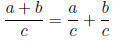
and the quotient rule for exponents
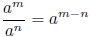
EX 12. Divide:
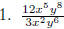
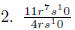
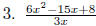
5.3.2 Divide a Polynomial by a Binomial
To divide two polynomials we use a procedure very similar to long division.
Let's look at examples:
EX 13. Divide: