HOW GRAND IS YOUR TOTAL
__ __ __
X __ __ __
Product C -----------------------
Grand Total
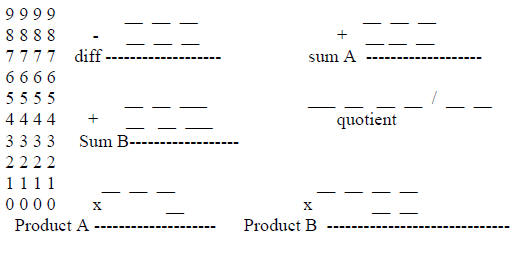
Sum A = _________
Sum B = ____________
Difference = _____________
Quotient = ______________
Product A= ____________
Product B = ___________
Product C= _____________
--------------------------------------
Total _____________
Source: Nancy Nutting
Lesson 3
MN Standard : Understanding operations and how they relate to one another.
This lesson investigates the operation of division.
1. First we must define the meaning of divisibility and
its relationship to multiplication. Also, establish the general rule for
divisibility of the numbers 2,3, and 5. At this point I will review the meaning
of ‘odd’ and ‘even’ numbers.
See if the students can give a definition for finding out
when they can tell if a number is divisible by 2,3, or 5.
2. Using 18/7 as an example relate this to the tradition
division algorithm box, such as used in long division. Set up the following
equation ________=________x________+________
And see if anyone can transform the 18/7 problem to fit the blanks in the above
equation. Then, see if they can establish which is the quotient, divisor,
dividend and remainder.
3. See if any student remembers the definition of a Prime
number.
Once the definition is established, show how to make a Prime factor tree for any
number such as 48 or 45. Point out that this method will be used many times in
this course.
4. It would be advisable to review a few examples of the
long division algorithm, such as 4756 / 57. This will cause problems for some
and tell them you will help them individually with this division.
5. For a group investigation into divisibility, have them
go through the ‘Sieve of Eratosthenes’ for the numbers up through 60. Explain
the first step of crossing out the numbers divisible by 2, except for the number
two. Have them then try the number three and so on. See if anybody can establish
what the numbers not crossed out represent.
6. For a take home number sense puzzle problem, which
takes some excellent thinking- pass out the “Flashlight Problem” given on the
next page. And if anyone can figure it out, let them explain it to the class at
the next session.
Announcement- at the end of next class will be a short readiness quiz from your
first 3 textbook assignments.
SUMMARY LESSON 3- In this lesson you should have
learned about divisibility, prime numbers and the relationship of multiplication
and division.
THE FLASHLIGHT PROBLEM
The Beatles have only 17 minutes left to get to their van
so they can make it to their next concert. To get to their van, they have to
cross a narrow bridge that only two of them can be on at a time. To make matters
even worse, it is pitch black out and they only have a single flashlight. Any
party of two who crosses the bridge must have the flashlight with them. The
flashlight must be walked across the bridge; it cannot be thrown.
It takes each of the Beatles a different amount of time to
cross the bridge, as noted:
Paul’s rate: 1 minute
John’s rate 2 minutes
Ringo’s rate 5 minutes
George’s rate 10 minutes
Any pair of Beatles who walk across must walk at the
slower one’s pace. For example, if John and Ringo walked across together, it
would take 5 minutes.
Explain how the ‘Fab-Four’ can get across the bridge in
the allotted 17 minutes in order to make it on time for their next concert.
No tricks are used to solve the problem . You can’t have
them swim, drive the van over and turn on the headlights, ride on each other’s
shoulders, build and new bridge, or any other tom-foolery. Just give it a try
and think outside the ?
Source: Greg Sarles,Bemidji State University
Lesson 4
MN standard: Understand the meaning of operations
and how they relate to each other.
This lesson is to understand the order of operations if
more than one occur in the same problem. These rules apply to not only whole
numbers, but to all phases of levels of mathematics. They will appear in most
problems you will occur in Math, Physics, Chemistry, Nursing, Business ect.
1. Understand the grouping symbols, parenthesis, Brackets ,
and the division line as used in fractions .
2. Review exponents 32 , 30, 3-2
3. Review Radicals mainly perfect squares, perfect cubes.
4. Now put to together the rules for operations for
example a problem like 2(8x5 – 36)3 + 15/3
1. Do what’s in the grouping symbols first in this case
inside the parenthesis . That means simplify inside the parenthesis.
2. Next apply any exponents.
3. Multiplication and Division are the next in the order and if both are in the
problem after doing steps 1 and 2, you do them in order from left to right.
4. Finally you do Addition or Subtraction . Again if both are in the same
problem, you do them in order from left to right.
For the class number sense investigation which will be a
good application we will use the 1-2-3-4 Challenge Work Sheet, which follows on
the next page.
The text assignment has some excellent problems on order
of operations. Remember to check your answers in the back of the text.
The last 15 minutes will be for Quiz #1 –the first 10
minutes will be done solo, the last 5 minutes together in groups to very
results.
Each individual must turn in a quiz with work shown.
SUMMARY LESSON 4 – While learning the important
rules of order of operation, we also covered definition of exponents and of
simple radicals mainly perfect squares and perfect cubes.
1-2-3-4 – Challenge
Use all four numbers: 1,2,3,4 only once
And any of the 4 operations +,-,x,/ and exponents to
Form expressions for
| 1 = |
5 = |
9= |
| 2 = |
6 = |
10 = |
| 3 = |
7 = |
11 = |
| 4 = |
8 = |
12 = |
From Texas Instruments copyright 2001



