Preface
The 1990s saw a wave of calculus reform whose aim was to teach students to think
for themselves and to solve substantial problems, rather than merely memorizing
formulas and performing rote algebraic manipulations. This book has a similar,
albeit somewhat more ambitious, goal, to lead you to think mathematically and
to experience the thrill of independent intellectual discovery. Our chosen
subject,
Number Theory , is particularly well suited for this purpose. The natural numbers
1, 2, 3, . . . satisfy a multitude of beautiful patterns and relationships, many
of
which can be discerned at a glance, others are so subtle that one marvels they
were
noticed at all. Experimentation requires nothing more than paper and pencil, but
many false alleys beckon to those who make conjectures on too scanty evidence.
It
is only by rigorous demonstration that one is finally convinced that the
numerical
evidence reflects a universal truth. This book will lead you through the groves
wherein lurk some of the brightest flowers of Number Theory, as it
simultaneously
encourages you to investigate, analyze, conjecture, and ultimately prove your
own
beautiful number theoretic results.
This book was originally written to serve as a text for Math 42, a course
created
by Jeff Hoffstein at Brown University in the early 1990s. Math 42 was designed
to
attract nonscience majors, those with little interest in pursuing the standard
calculus
sequence, and to convince them to study some college mathematics. The intent was
to create a course similar to one on, say, “The Music of Mozart” or “Elizabethan
Drama,” wherein an audience is introduced to the overall themes and methodology
of an entire discipline through the detailed study of a particular facet of the
subject.
Math 42 has been extremely successful, attracting both its intended audience and
also scientifically oriented undergraduates interested in a change of pace from
their
large-lecture, cookbook-style courses.
The prerequisites for reading this book are few. Some facility with high school
algebra is required , and those who know how to program a computer will have fun
generating reams of data and implementing assorted algorithms, but in truth the
reader needs nothing more than a simple calculator . Concepts from calculus are
mentioned in passing, but are not used in an essential way. However, and the
reader
is hereby forewarned, it is not possible to truly appreciate Number Theory
without
an eager and questioning mind and a spirit that is not afraid to experiment, to
make
mistakes and profit from them, to accept frustration and persevere to the
ultimate
triumph. Readers who are able to cultivate these qualities will find themselves
richly rewarded, both in their study of Number Theory and their appreciation of
all
that life has to offer.
Acknowledgments for the First Edition
There are many people I would like to thank for their assistance—Jeff Hoffstein,
Karen Bender, and Rachel Pries for their pioneering work in Math 42, Bill Amend
for kindly permitting me to use some of his wonderful FoxTrot cartoons, the
creators
of PARI for providing the ultimate in number theory computational power ,
Nick Fiori, Daniel Goldston, Rob Gross, Matt Holford, Alan Landman, Paul
Lockhart,
Matt Marcy, Patricia Pacelli, Rachel Pries (again), Michael Schlessinger,
Thomas Shemanske, Jeffrey Stopple, Chris Towse, Roger Ware, Larry Washington,
Yangbo Ye, and Karl Zimmerman for looking at the initial draft and offering
invaluable suggestions, Michael Artin, Richard Guy, Marc Hindry, Mike Rosen,
Karl Rubin, Ed Scheinerman, John Selfridge, and Sam Wagstaff for much helpful
advice, and George Lobell and Gale Epps at Prentice Hall for their excellent
advice
and guidance during the publication process.
Finally, and most important, I want to thank my wife Susan and children Debby,
Daniel, and Jonathan for their patience and understanding while this book was
being written.
Acknowledgments for the Second Edition
I would like to thank all those who took the time to send me corrections and
suggestions
that were invaluable in preparing this second edition, including Arthur Baragar,
Aaron Bertram, Nigel Boston, David Boyd, Seth Braver, Michael Catalano-
Johnson, L. Chang, Robin Chapman, Miguel Cordero, John Cremona, Jim Delany,
Lisa Fastenberg, Nicholas Fiori, Fumiyasu Funami, Jim Funderburk, Andrew
Granville, Rob Gross, Shamita Dutta Gupta, Tom Hagedorn, Ron Jacobowitz, Jerry
S. Kelly, Hershy Kisilevsky, Hendrik Lenstra, Gordon S. Lessells, Ken Levasseur,
Stephen Lichtenbaum , Nidia Lopez Jerry Metzger, Jukka Pihko, Carl Pomerance,
Rachel Pries, Ken Ribet, John Robeson, David Rohrlich, Daniel Silverman, Alfred
Tang, and Wenchao Zhou.
Acknowledgments for the Third Edition
I would like to thank Jiro Suzuki for his beautiful translation of my book into
Japanese. I would also like to thank all those who took the time to send me
corrections
and suggestions that were invaluable in preparing this third edition, including
Bill Adams, Autumn Alden, Robert Altshuler, Avner Ash, Joe Auslander,
Dave Benoit, J¨urgen Bierbrauer, Andrew Clifford, Keith Conrad, Sarah DeGooyer,
Amartya Kumar Dutta, Laurie Fanning, Benji Fisher, Joe Fisher, Jon Graff, Eric
Gutman, Edward Hinson, Bruce Hugo, Ole Jensen, Peter Kahn, Avinash Kalra,
Jerry Kelly, Yukio Kikuchi, Amartya Kumar, Andrew Lenard, Sufatrio Liu, Troy
Madsen, Russ Mann, Gordon Mason, Farley Mawyer, Mike McConnell, Jerry
Metzger, Steve Paik, Nicole Perez, Dinakar Ramakrishnan, Cecil Rousseau, Marc
Roth, Ehud Schreiber, Tamina Stephenson, Jiro Suzuki, James Tanton, James Tong,
Chris Towse, Roger Turton, Fernando Villegas, and Chung Yi.
Email and Electronic Resources
All the people listed above have helped me to correct numerous mistakes and to
greatly refine the exposition, but no book is ever free from error or incapable
of
being improved. I would be delighted to receive comments, good or bad, and
corrections from my readers.
Introduction
Euclid alone
Has looked on Beauty bare. Fortunate they
Who, though once only and then but far away,
Have heard her massive sandal set on stone.
Edna St. Vincent Millay (1923)
The origins of the natural numbers 1, 2, 3, 4, 5, 6, . . . are lost in the mists
of
time. We have no knowledge of who first realized that there is a certain concept
of
“threeness” that applies equally well to three rocks, three stars, and three
people.
From the very beginnings of recorded history, numbers have inspired an endless
fascination—mystical, aesthetic, and practical as well. It is not just the
numbers
themselves, of course, that command attention. Far more intriguing are the
relationships
that numbers exhibit, one with another. It is within these profound and
often subtle relationships that one finds the Beauty so strikingly described in
Edna
St. Vincent Millay’s poem. Here is another description by a celebrated
twentieth-century
philosopher.
Mathematics, rightly viewed, possesses not only truth, but supreme
beauty—a beauty cold and austere, like that of sculpture, without appeal
to any part of our weaker nature, without the gorgeous trappings
of paintings or music, yet sublimely pure, and capable of a stern perfection
such as only the greatest art can show. (Bertrand Russell, 1902)
The Theory of Numbers is that area of mathematics whose aim is to uncover
the many deep and subtle relationships between different sorts of numbers. To
take
a simple example, many people through the ages have been intrigued by the square
numbers 1, 4, 9, 16, 25, . . . . If we perform the experiment of adding together
pairs
of square numbers, we will find that occasionally we get another square. The
most
famous example of this phenomenon is
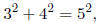
but there are many others, such as
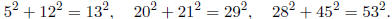
Triples like (3, 4, 5), (5, 12, 13), (20, 21, 29), and
(28, 45, 53) have been given the
name Pythagorean triples. Based on this experiment, anyone with a lively
curiosity
is bound to pose various questions, such as “Are there infinitely many
Pythagorean
triples?” and “If so, can we find a formula that describes all of them?” These
are the sorts of questions dealt with by number theory.
As another example, consider the problem of finding the remainder when the
huge number
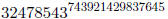
is divided by 54817263. Here’s one way to solve this
problem. Take the number
32478543, multiply it by itself 743921429837645 times, use long division to
divide
by 54817263, and take the remainder. In principle, this method will work,
but in practice it would take far longer than a lifetime, even on the world’s
fastest
computers. Number theory provides a means for solving this problem, too. “Wait a
minute,” I hear you say, “Pythagorean triples have a certain elegance that is
pleasing
to the eye, but where is the beauty in long division and remainders?” The
answer is not in the remainders themselves, but in the use to which such
remainders
can be put. In a striking turn of events, mathematicians have shown how the
solution of this elementary remainder problem (and its inverse) leads to the
creation
of simple codes that are so secure that even the National Security Agency
is unable to break them. So much for G.H. Hardy’s singularly unprophetic remark
that “no one has yet discovered any warlike purpose to be served by the theory
of
numbers or relativity, and it seems very unlikely that anyone will do so for
many
years.”
The land of Number Theory is populated by a variety of exotic flora and fauna.
There are square numbers and prime numbers and odd numbers and perfect numbers
(but no square-prime numbers and, as far as anyone knows, no odd-perfect
numbers). There are Fermat equations and Pell equations, Pythagorean triples and
elliptic curves, Fibonacci’s rabbits, unbreakable codes, and much, much more.
You
will meet all these creatures, and many others, as we journey through the Theory
of Numbers.



