0. Two evenly matched teams play in the world series, a best of seven
competition in which the competition
stops as soon as one team has won four games. Is the world series more likely to
end in six or seven games?
1.[2004-A5] An m × n checkerboard is colored randomly: each square is
independently assigned red or
black with probability 1/2. We say that two squares , p and q, are in the same
connected monochromatic
component if there is a sequence of squares , all of the same color, starting at
p and ending at q, in which
successive squares in the sequence share a common side. Show that the expected
number of connected
monochromatic regions is greater than mn/8.
2.[2002-B1] Shanille O’Keal shoots free throws on a basketball court.
She hits the first and misses the
second, and thereafter the probability that she hits the next shot is equal to
the proportion of shots she has
hit so far. What is the probability she hits exactly 50 of her first 100 shots?
3.[2002-B4] An integer n, unknown to you, has been randomly chosen in
the interval [1, 2002] with uniform
probability. Your objective is to select n in an odd number of guesses . After
each incorrect guess, you are
informed whether n is higher or lower , and you must guess an integer on your
next turn among the numbers
that are still feasibly correct. Show that you have a strategy so that the
chance of winning is greater than
2/3.
4.[2001-A2] You have coins C1,C2, . . . ,Cn. For each k, Ck is biased
so that, when tossed, it has probability
1/(2k + 1) of falling heads. If the n coins are tossed, what is the probability
that the number of heads is
odd? Express the answer as a rational function of n.
5.[1993-B3] Two real numbers x and y are chosen at
random in the interval (0,1) with respect to the
uniform distribution . What is the probability that the closest integer to x/y is
even? Express the answer in
the form r + sπ, where r and s are rational numbers .
6.[1992-A6] Four points are chosen at random on the
surface of a sphere. What is the probability that the
center of the sphere lies inside the tetrahedron whose vertices are at the four
points? (It is understood that
each point is independently chosen relative to a uniform distribution on the
sphere .)
7.[1989-A4] If is an irrational number, 0 < α < 1,
is there a finite game with an honest coin such that
the probability of one player winning the game is α? (An honest coin is one for
which the probability of
heads and the probability of tails are both 1/2 . A game is finite if with
probability 1 it must end in a finite
number of moves .)
8.[1989-B1] A dart, thrown at random, hits a square
target. Assuming that any two parts of the target of
equal area are equally likely to be hit , find the probability that the point hit
is nearer to the center than to
any edge. Express your answer in the form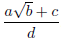
,
where a, b, c, d are integers.
9.[1985-B4] Let C be the unit circle x^2 + y^2 = 1.
A point p is chosen randomly on the circumference C
and another point q is chosen randomly from the interior of C (these points are
chosen independently and
uniformly over their domains). Let R be the rectangle with sides parallel to the
x and y-axes with diagonal
pq. What is the probability that no point of R lies outside of C?
10.[1982-B3] Let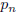 
be the probability that c+d is a perfect square when the integers c and d are
selected
independently at random from the set {1, 2, . . . , n}. Show that
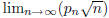exists, and express this limit
in the form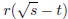 
, where s and t are integers and
r is a rational number .
11. Let π be a random permutation of the numbers 1, 2, . .
. , n. What is the expected length of the cycle
containing 1?
12. Le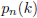t 
be the number
of permutations of {1, 2, . . . , n} which have exactly k fixed points. Prove
that
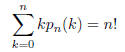
(i. e. the expected number of fixed points of a random
permutation is 1).
