Sample Math Problems

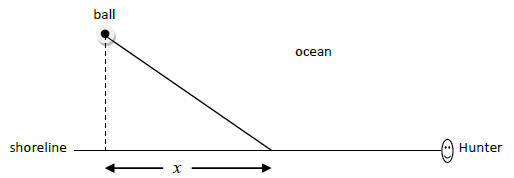
9. Mark and his dog Hunter are standing together on the shore at the beach. Mark throws a ball
into the ocean and Hunter runs along the shoreline until some point in which he enters the
water and swims to retrieve the ball. The ball enters the water 200 feet down the shoreline
from where they stand and 50 feet from the shore. Hunter can run 8.8 feet per second along
the shore but can only swim 3.6 feet per second in the ocean. At what point along the shore
should Hunter enter the water in order to minimize his total time?

Let x represent the distance from where Hunter enters the water to the point on the shore
opposite the ball.

(a) Write an expression in terms of x that represents
the distance Hunter will run along the shore. ……………………………
the distance that Hunter swims …………………………………………...
(b) The total time it takes Hunter to reach the ball is given by
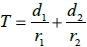
where 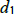= the distance Hunter runs along the shore, 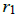= the rate at which Hunter runs,
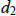= the distance Hunter swims and 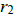= the rate at which Hunter swims. Write a
function of T in terms of x .

(c) At what point should Hunter enter the water in order to minimize the time it takes him to
reach the ball? Document your process for answering this question.

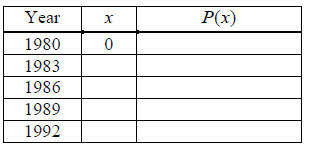
10. In 1980, the average price of a house in a certain county was $80,000. Prices have increased
at an average rate of 5% every three years. Let P(x) represent the price of a house in this
county x years after 1980.

(a) Complete the table below:

(b) Write an algebraic representation for P(x) using fractional exponents.

(c) Find the exponential regression model for this data. What does the regression model
suggest about the growth rate of housing prices in this time period?

(d) How could you have predicted the regression model from your answer to (b)?

(e) How much will a house sell for in 2000? Document your process.

(f) When will a house be worth $150,000? Document your process.

11. Miranda bought a truck for $40,000 with an expected half-life of 3 years.

(a) Complete the table below.

(b) Write an algebraic model for this problem situation using fractional exponents. Define
your variables .

(c) Find an exponential regression model for the table above.

(d) What is the annual depreciation of this truck?

(e) Explain why the algebraic model and the regression model are equivalent?

12. The interest formula for compounding n times a year is given by .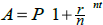

(a) How much money will Jason accrue in 10 years if he deposits $10,000 in an account
paying 6% compounded monthly?

(b) How long will it take $5000 to double in value if it is deposited into a certificate of
deposit that pays 4.5% compounded quarterly?

13. (a) Write 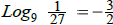in exponential form. Then verify the result using what you know
about fractional exponents ( not your calculator ).

(b) Change from exponential to logarithmic for , or vice versa. Solve for the variable.

Exponential Form	Logarithmic Form	Solution for variable

(c) Use your properties of logarithms to write equivalent expressions for each of the
following. Simplify your expression whenever possible. Each equivalent expression will
contain either an x or log x and other constants.

14. Biologists often model population growth using the number e since this is continuous
reproduction in populations in normal circumstances. A group of biologist studying
chickadee populations in West Texas estimate that currently there are approximately half a
million chickadees in the region. Based on past studies, they estimate that the population is
growing at a continuous rate of 34.66% each year. Thus the chickadee population can be
modeled by the function 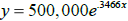, where x is the number of years from now and y
is the Chickadee population.

(a) How long does it take the chickadee population to double?

(b) Make a table that shows the chickadee population for a 5-year period.

(c) What pattern do you notice in the table? Write another model for the population growth
based on this pattern.

(d) Explain why the two models you have constructed are equivalent?

15. A bit more skill practice  True / False or Fill in the blank.

a) ln 7 means 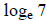. True False

b) The expression x(x + 4) + 7 is in factored form . True False
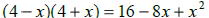True False
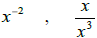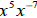c) , and are equivalent expressions . True False

d) The opposite of 4 – x is x – 4. True False

e) A rational expression is a fraction whose numerator and denominator can be factored.
True False

f) 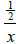is equivalent to 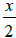True False

g) The product of any complex number and its conjugate is always a real number .
True False

h) What number must be added to both sides of x² – 14x = 20 to “complete the
square”? …………………….

i) 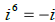True False

j) 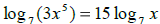True False

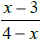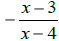k) The expressions and are equivalent. True False

l) The x- coordinate of the vertex of the parabola y = 4x² – 12x + 11 is
……………………

m) 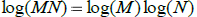True False
n) The expression 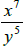can be simplified by subtracting exponents True False
o) The domain of 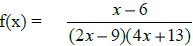is………………………..

p) The difference of squares A²– B² can be factored as …………………………….

q) 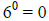True False

r) The expression 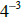represents a negative number . True False