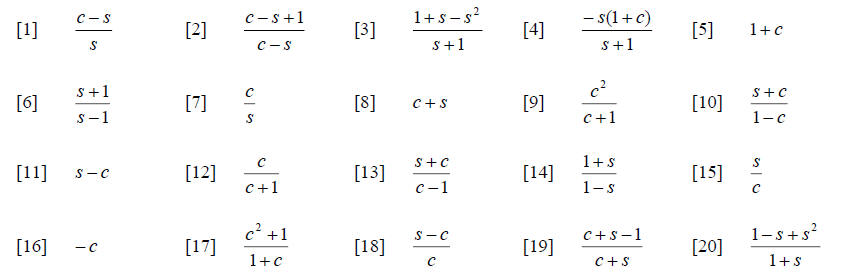Complex fractions are fractions in which the numerator or
denominator, or both, contain fractions. They are critical to
analytic trigonometry and identity proving, because each individual
trigonometric function can be expressed as a
fraction involving other trigonometric functions . Whenever a complex fraction
appears, you should simplify it
immediately, before you use it in any other operation . Otherwise, you risk
making a straightforward problem
exponentially more difficult .
There are 2 primary ways to simplify complex fractions.
METHOD 1: Write the numerator and denominator each as a
single fraction, then perform the implied division .
METHOD 2: Multiply the numerator and denominator by the
LCD of all the component fractions.
You should try both, and decide which is more
natural for you.
Simplify the following.
NOTE: c and s represent variables . Do NOT assume they mean cos x or
sin x .
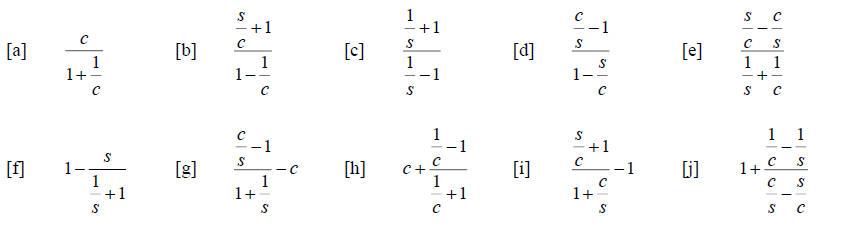
Some possible answers to choose from:
NOTE: half of these answers are not correct of any of the problems above
(from numerator),
and
(from denominator)
