Inequality-Solve, Apply
4.1 Inequality – Solve, Apply
Need To Know
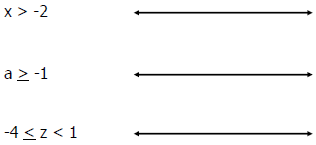
Graphing inequalities
Addition property of inequality
Multiplication property of inequality
Solving inequalities
Graphing Inequalities
Graph each:
Solving Inequalities - Rules
Multiplication Property of Equality
1) If A < B,
Then AC < BC if C is positive.
Multiplying or dividing a positive to both sides of the
inequality will keep the same solution set.
2) If A < B,
Then AC > BC if C is negative .
Solving Inequalities
Solve and graph:
2(3m – 1) + 5 ≥ 8m – 7
Metro Concerts can rent a truck for either $55 with
unlimited
mileage or $29 plus 40ยข per mile.
For what mileage would the unlimited mileage plan be better?
4.2 Intersection, Union, Compound
Need To Know
Intersections as:
1. Set (explain but not doing set builder notation)
2. Graph
3. Interval
Union as:
1. Set
2. Graph
3. Interval
Compound Inequalities
4.2 has lots of new ideas, read and study hard
Intersection A ∩ B
Here are some new ideas about sets.
The intersection of A and B is a set of numbers
that are COMMON to both A and B. Written ∩
( logically the same as “AND” and sometimes called a conjunction.)
| Example: Interval and graph
Find all x’s for which
x ≥ -3 and x < 2
|
 |
Union A ∪ B
The union of A and B is a set of all numbers from
COMBINING A and B into one set. Written ∪
(logically the same as “OR”; and sometimes called a disjunction.)
Example: Interval and graph
Find all x’s for which
x ≤ -1 or x > 2 |
|
Solving Compound Inequalities
Solve and Graph - Realize this form is “AND”.
-11 < 2n – 3 ≤ -5
Solve and Graph
g(x) < -2 or g(x) ≥ 10, where g(x) = 3x – 5.
end
4.3 Solve Abs. Value Eq . & Ineq.
Need To Know
Recall Absolute Value
Solve
Absolute Value Equations
Absolute Value Inequalities
Absolute Value
Recall:
Absolute Value, |x|,
Solving Equation
| Solve: |
Solving Equation Principle : |
 |
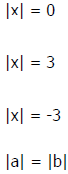1) |x| = 0 means |
| 2) |x| = p means |
| 3) |x| = neg. ____________ |
| 4) |a| = |b| means |
Solve Abs. Value Equations
Solve:
|2x – 3| = 4
Find all x’s for f(x) = 2 where
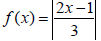
Solve:
|x + 4| = |x – 3|
Solve
|x| < 3 |
Solving Inequality Principle
1) |x| < p means |
| Solve: 7 + |4a + 5| <
26 |
|
Solve
|x| < 3 |
Solving Inequality Principle
1) 2) |x| > p means |
| Solve: |3z + 4| + 2 >
8 |
|
4.4 Graphing Linear Ineq
Need To Know
Idea of linear inequalities
How to graph linear inequalities
How to graph systems of linear inequalities
Apply
How to Graph Linear Inequalities
Graphing Linear Inequalities - Detailed
Graph the boundary line
A) Decide if the line is included in the solutions set or not.
< or > means the line is not in solutions –
dashed line
≤ or > means the line is a solutions –
solid line
B) Make the inequality into an equation (=) and graph it.
Shade the solution side of the boundary line
A) Pick a test point not on the line
B) Plug it into the original inequality and evaluate true or false
C) Shade the side containing the point making the inequality true.
Practice
Graph:
x + y < 4
Graph:
x ≥ 3
Graph the system:
-3 ≤ y < 2
Graph the system :
x + y < 1
x - y ≤ 2
