Problem: Let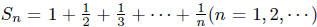 
.
Prove that 
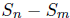is never an
integer for m < n.
(Hint: for any k, between k and 2k there is at least one prime number .)
Solution (by Kedar Hippalgaonkar, Fr. ME; this is his second solution,
which makes no
use of the given hint; it is edited by the panel)
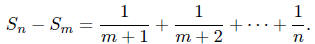
If 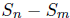is an integer then
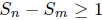hence n ≥ 2m. There is a largest power
of 2,
say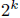 
between (m+1) and n, because if
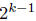is largest power of 2 less than (m+1) then
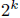is between (m+ 1) and n.
The LCM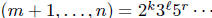 
. So
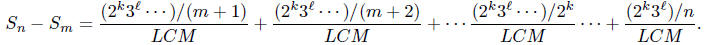
All the numerators are divisible by 2, except one, hence
the sum is odd , while denominator
is even. 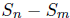is not an integer.
Also solved by :
Undergraduates: Jason Anema (Jr. MA), Jignesh V. Mehta (So. Phys)
Graduates: Jianguang Guo (Phys)
Faculty: Steven Landy (Physics at IUPUI)
Others: Georges Ghosn (Quebec), Andrew Klein (Omaha), Chris Lomont (Cybernet,
Ann
Arbor, MI), Namig Mammadov (Baku, Azerbaijan), Angel Plaza (ULPGC Spain)
Two incorrect solutions were received.
Late solutions for Problem 13 from graduate students Jianguang Guo (Physics) and
Gaurav
Sharma (ECE).
