Geometry - Grade 12
42.1 Introduction
Activity :: Discussion : Discuss these Research Topics
Research one of the following geometrical ideas and describe it to your group :
1. taxicab geometry,
2. sperical geometry,
3. fractals,
4. the Koch snowflake.
42.2 Circle Geometry
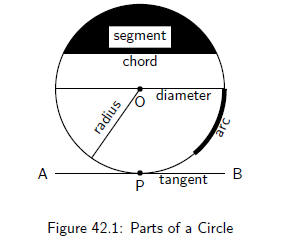
42.2.1 Terminology
The following is a recap of terms that are regularly used
when referring to circles.
arc An arc is a part of the circumference of a
circle.
chord A chord is defined as a straight line joining the ends of an arc.
radius The radius, r, is the distance from the centre of the circle to
any point on the circum-
ference.
diameter The diameter ΓΈ is a special chord that
passes through the centre of the circle. The
diameter is the straight line from a point on the circumference to another point
on the
circumference, that passes through the centre of the circle.
segmebt A segment is the part of the circle that is
cut off by a chord. A chord divides a circle
into two segments .
tangent A tangent is a line that makes contact with
a circle at one point on the circumference.
(AB is a tangent to the circle at point P.
42.2.2 Axioms
An axiom is an established or accepted principle. For this section, the
following are accepted as
axioms.
1. The Theorem of Pythagoras, which states that the square
on the hypotenuse of a right-
angled triangle is equal to the sum of the squares on the other two sides. In
△ABC, this
means that AB2 + BC2 = AC2
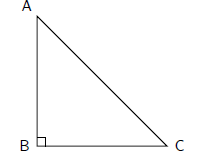
Figure 42.2: A right-angled triangle
2. A tangent is perpendicular to the radius, drawn at the
point of contact with the circle.
42.2.3 Theorems of the Geometry of Circles
A theorem is a general proposition that is not self-evident but is proved by
reasoning (these
proofs need not be learned for examination purposes).
Theorem 6. The line drawn from the centre of a
circle, perpendicular to a chord, bisects the
chord.
Proof:
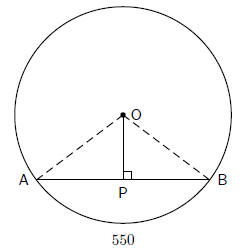
Consider a circle, with centre O. Draw a chord AB and draw a perpendicular line
from the
centre of the circle to intersect the chord at point P.
The aim is to prove that AP = BP
1. △OAP and △OBP are right-angled triangles.
2. OA = OB as both of these are radii and OP is common to both triangles.
Apply the Theorem of Pythagoras to each triangle, to get:
OA2 = OP2 + AP2
OB2 = OP2 + BP2
However, OA = OB. So,
OP2 + AP2 = OP2 + BP2
AP2 = BP2
and AP = BP
This means that OP bisects AB.
Theorem 7. The line drawn from the centre of a
circle, that bisects a chord, is perpendicular
to the chord.
Proof:
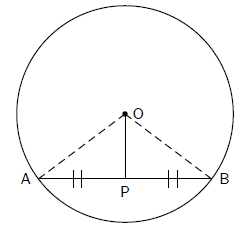
Consider a circle, with centre O. Draw a chord AB and draw a line from the
centre of the circle
to bisect the chord at point P.
The aim is to prove that OP ⊥ AB
In △OAP and △OBP,
1. AP = PB (given)
2. OA = OB (radii)
3. OP is common to both triangles.
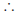△OAP ≡ △OBP (SSS).
Theorem 8. The perpendicular bisector of a chord
passes through the centre of the circle.
Proof:
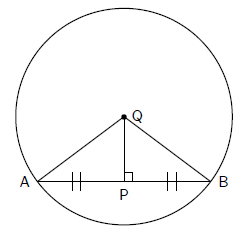
Consider a circle. Draw a chord AB. Draw a line PQ perpendicular to AB such that
PQ bisects
AB at point P. Draw lines AQ and BQ.
The aim is to prove that Q is the centre of the circle,
by showing that AQ = BQ.
In △OAP and △OBP,
1. AP = PB (given)
3. QP is common to both triangles.
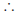△QAP ≡ △QBP (SAS).
From this, QA = QB. Since the centre of a circle is the
only point inside a circle that has points
on the circumference at an equal distance from it, Q must be the centre of the
circle.
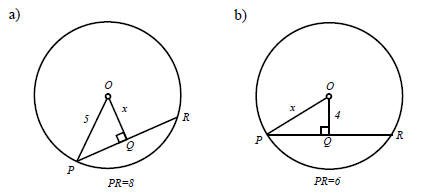
Exercise: Circles I
1. Find the value of x:
Theorem 9. The angle subtended by an arc at the centre of a circle is
double the size of the
angle subtended by the same arc at the circumference of the circle.
Proof:
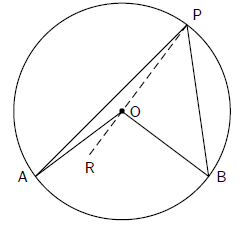
Consider a circle, with centre O and with A and B on the circumference. Draw a
chord AB.
Draw radii OA and OB. Select any point P on the circumference of the circle.
Draw lines PA
and PB. Draw PO and extend to R.
The aim is to prove that
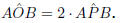
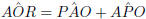(exterior angle = sum of interior opp.
angles)
But,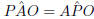 
(△AOP is an isosceles △)
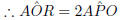
Similarly,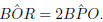 
So,
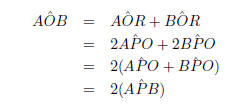
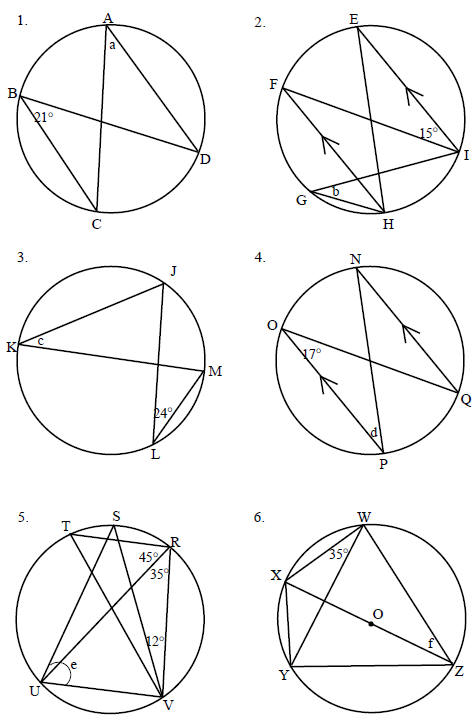
Exercise: Circles II
1. Find the angles (a to f) indicated in each diagram:
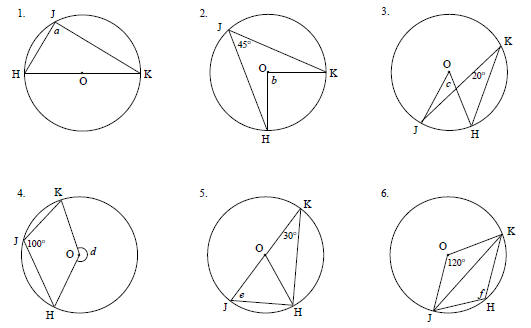
Theorem 10. The angles subtended by a chord at the circumference of a
circle on the same
side of the chord are equal.
Proof:
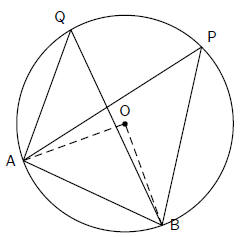
Consider a circle, with centre O. Draw a chord AB. Select any points P and Q on
the
circumference of the circle, such that both P and Q are on the same side of the
chord. Draw
lines PA, PB, QA and QB.
The aim is to prove that
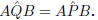
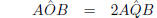
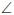at centre = twice
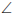at circumference
and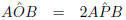 
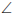at
centre = twice 
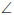at circumference
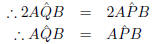
Theorem 11. (Converse of Theorem 10) If a line
segment subtends equal angles at two other
points on the same side of the line, then these four points lie on a circle.
Proof:
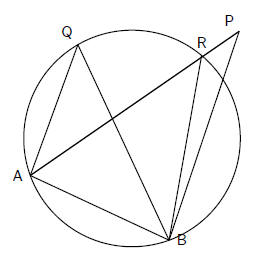
Consider a line segment AB, that subtends equal angles at points P and Q on the
same side of
AB.
The aim is to prove that points A, B, P and Q lie on
the circumference of a circle.
By contradiction. Assume that point P does not lie on a
circle drawn through points A, B and
Q. Let the circle cut AP (or AP extended) at point R.
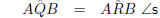on same side of chord
but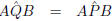
(given)
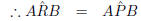
but this cannot be true since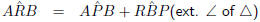 
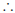the assumption that the
circle does not pass through P, must be false, and A, B, P and Q
lie on the circumference of a circle.
Exercise: Circles III
1. Find the values of the unknown letters.
Cyclic Quadrilaterals
Cyclic quadrilaterals are quadrilaterals with all four
vertices lying on the circumference of a circle.
The vertices of a cyclic quadrilateral are said to be concyclic.
Theorem 12. The opposite angles of a cyclic
quadrilateral are supplementary.
Proof:
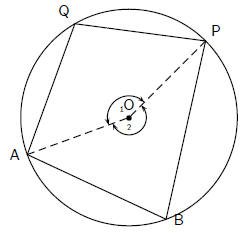
Consider a circle, with centre O. Draw a cyclic quadrilateral ABPQ. Draw AO
and PO.
The aim is to prove that
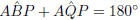and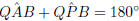 
.
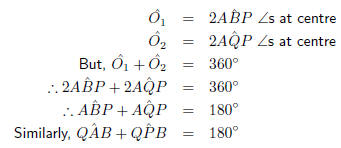
Theorem 13. (Converse of Theorem 12) If the opposite angles of a quadrilateral
are supplementary,
then the quadrilateral is cyclic.
Proof:
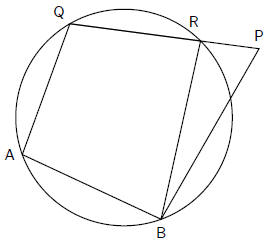
Consider a quadrilateral ABPQ, such that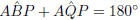
and .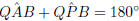
The aim is to prove that points A, B, P and Q lie on the circumference of a
circle.
By contradiction. Assume that point P does not lie on a circle drawn through
points A, B and
Q. Let the circle cut AP (or AP extended) at point R. Draw BR.
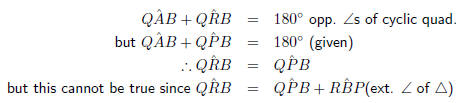
the assumption that the circle does not pass through P, must be false, and A,
B, P and Q
lie on the circumference of a circle and ABPQ is a cyclic quadrilateral.
