Appendix A: The Laws of Exponents
Exponents are a short -hand notation used to represent many
factors multiplied together. All
of the rules for manipulating exponents may be deduced from the laws of
multiplication and
division that you are already familiar with.
Exponential notation
Repeated multiplication is represented using exponential
notation, for example:
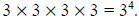
There are four factors in the product , each of which is a
3. In the mathematical expression
34, 4 is called the exponent and 3 is usually called the base.
For a real number a and a positive integer n, exponentials
are defined by:
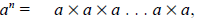
a total of n factors, each of which is an a.
A special case of exponential notation to note:
a1 = a.
This makes sense, since a1 should have only one factor of
a .
Rules for combining exponents
Suppose that a and b are real numbers and that m and n are
positive integers.
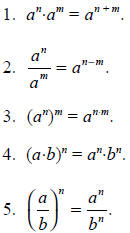
Justifications of these laws are based on the laws of multiplication and
division that you are
familiar with. Rules 1, 3 and 4 are justified below, and the ideas of the
justifications for
Rules 2 and 4 described. (The justifications of Rules 2 and 4 are exercises for
this
appendix.)
For the first exponential rule,
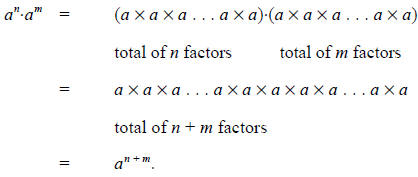
For the third exponential rule,
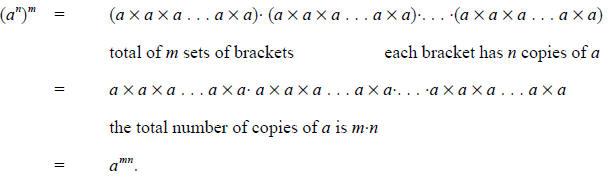
For the fourth exponential rule,
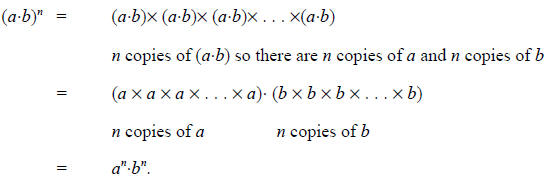
The idea for justifying second exponential rule is this: there are n copies of a
in the
numerator of the fraction , and m copies of a in the denominator of the fraction .
Some of
these copies of a will cancel out.
Lastly, the idea for the justification of the fifth exponential rule is this:
there are n copies of
the fraction a/b . Thus, the numerator will consist of n copies of a multiplied together, so
the
numerator is an. The denominator will consist of n copies of b multiplied
together, so the
denominator is bn. (To review concepts such as numerator, denominator and
multiplication
of fractions, see Appendix E.)
Many of these rules also work when m and n are not positive integers - for
example, if m
and n are fractions. Some special considerations apply when m and n are not
positive
integers in order to make sure that the expression makes good mathematical
sense. For
example, while it is possible to write down a collection of symbols like :
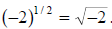
The collection of symbols
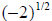 should represent the number that is the square
root of
should represent the number that is the square
root of
negative two. However, since squaring any real number gives a result that is
greater than or
equal to zero , there is no real number that, when squared, gives -2. While it is
possible to
write down the collection of symbols:
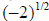 , there is no real number that
equals this
, there is no real number that
equals this
collection of symbols.
Example A.1
Use the laws of exponents to simplify the following algebraic expressions when
possible.
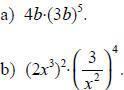
Solution :
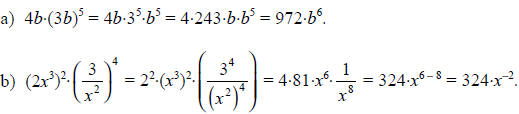
Part (b) illustrates an interesting point - the application of the exponent
rules can generate
algebraic expressions such as 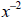 , which we have no way of interpreting at this
point.
, which we have no way of interpreting at this
point.
Interpreting and simplifying fractional and negative exponents
The way that we defined exponential notation as a short-hand for repeated
multiplication
makes complete sense for exponents that are positive integers. However, exactly
what an
expression like 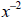 should mean is not so clear.
should mean is not so clear.
Let a be a real number, and let m and n be positive integers.
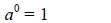 (provided that a
≠ 0)
(provided that a
≠ 0)
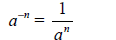 (provided that a
≠ 0)
(provided that a
≠ 0)
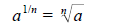 (if n is an even integer, then this only makes sense when a
≥ 0)
(if n is an even integer, then this only makes sense when a
≥ 0)
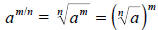 (if n is an even integer, then this only makes sense when a
≥ 0)
(if n is an even integer, then this only makes sense when a
≥ 0)
Example A.2
Using the laws of exponents, simplify the following expressions as much as
possible.
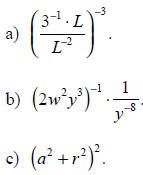
Solution:
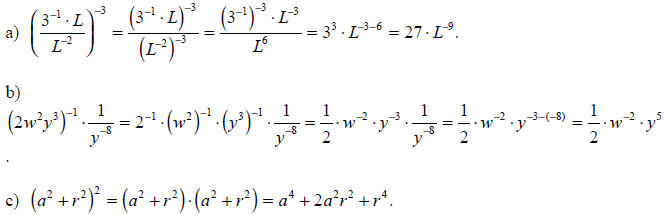
The important point in Part (c) is that there in no exponential rule that is
valid when the
terms inside the bracket are added (rather than multiplied or divided) together.
In particular,
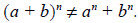
The important thing to remember here that that (a + b)n and an + bn are not the
same. (To
review the expansion of complicated algebraic expressions, see Appendix B.)
Example A.3
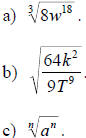
Solution:
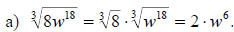 b)
b)
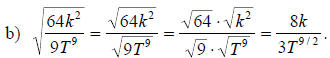
c) The simplification of
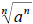 is not completely straight-forward. If a is a
positive number
is not completely straight-forward. If a is a
positive number
or zero, then
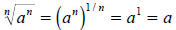
as you might expect. If a is a negative number, then the situation is more
complicated. If n
is an odd number, then
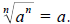 To illustrate this consider the case where n =
3 and a =
To illustrate this consider the case where n =
3 and a =
-2,
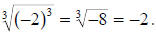
If n is an even number, then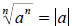 To illustrate this consider the case
where n = 2 and
To illustrate this consider the case
where n = 2 and
a = -2,
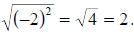
Exercises for Appendix A
For Problems 1-10, evaluate the quantity (if possible) without using a
calculator .
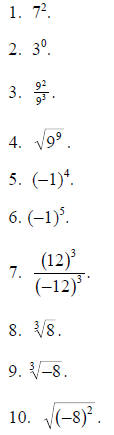
For Problems 11-20, simplify the expression as much as possible.
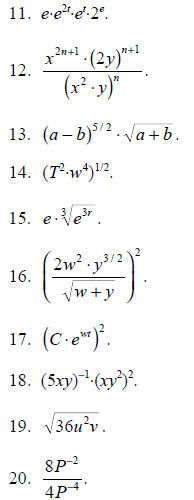
For Problems 21-25, decide whether each of the statements are true or false.
In problems 26 and 27 you will justify the last two exponential rules.
26. Suppose that a is a real number, and that n and m are positive integers.
Explain why:
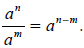
27. Suppose that a and b are real numbers, and that n is a positive integer.
Explain why:
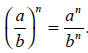
Answers to Exercises for Appendix A
26. The basic idea here is cancellation of common factors from the numerator and
denominator. There are n factors of a in the numerator and m factors of a in the
denominator. In the case where n > m, all of the factors of a in the denominator
will cancel with factors of a in the numerator, leaving n - m factors of a
remaining
in the numerator. In the case where n < m, the n factors of a in the numerator
will
cancel with factors in the denominator, leaving m - n factors of a in the
denominator. Thus, the simplified expressions will be:
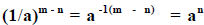
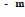 .
.
27. The basic idea here is that you will have n factors, each of which is a/b.
Thus,
the overall numerator will consist of n copies of a all multiplied together,
i.e. the
overall numerator is an. Similarly, the overall denominator is bn.



