Definition of a Rational Number
The set of rational numbers is the set 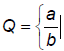 a and
b are integers,
a and
b are integers,
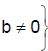
Equality of Rational Numbers
Let 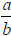 and
and 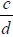 be any rational numbers. Then
be any rational numbers. Then 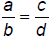 if and only if
ad = bc.
if and only if
ad = bc.
Simplest Form of a Rational Number
A rational number is in simplest form when the numerator and denominator are
both
integers that have no common factors other than 1 and the denominator is greater
than
zero.
Addition of Rational Numbers
Let 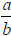 and
and 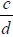 be
any rational numbers. Then
be
any rational numbers. Then 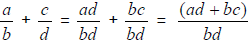
Properties of Addition of Rational Numbers
Closure Property
For rational numbers 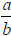 and
and
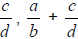 is a unique rational number.
is a unique rational number.
Commutative Property
For rational number 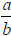 and
and
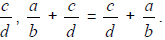
Associative Property
For rational numbers
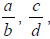 and
and 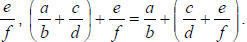
Identity Property
A unique rational number; 0, exists such that 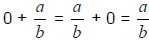 for every rational
for every rational
number 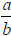 ; 0 is the additive identity element.
; 0 is the additive identity element.
Additive Inverse Property
For every rational number 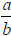 , a unique rational
number -
, a unique rational
number -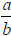 exists such that
exists such that
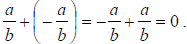
Subtraction of Rational Numbers: Adding the opposite
Let 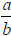 and
and
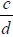 be any rational
numbers. Then
be any rational
numbers. Then
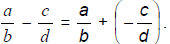
Multiplication of Rational Numbers
Let 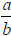 and
and
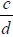 be any rational
numbers. Then
be any rational
numbers. Then 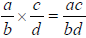
Basic Properties for Multiplication of Rational Numbers
The basic properties of multiplication for integers hold for rational numbers:
(Closure property, Identity property, Zero property , Commutative property,
Associative
property, and Distributive property )
BUT …. A new basic property of multiplication appears for rational numbers, a
property that didn’t exist for integers.
Multiplicative inverse or reciprocal
For every nonzero rational number 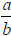 , a unique
rational number,
, a unique
rational number, 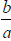 , exists such that
, exists such that
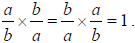
Division of Rational Numbers
Let 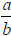 and
and
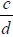 be any rational
numbers where
be any rational
numbers where 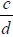 is
nonzero. Then
is
nonzero. Then 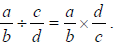
Using Models to Compare Rational Numbers
Fraction wall
Number Line
Common Positive Denominator
Approach
For rational numbers 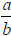 and
and
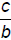 , where b > 0,
, where b > 0,
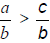 if and only if a > c.
if and only if a > c.
When the denominators of two rational numbers are the same, the one with the
greater
numerator represents the larger rational number.
Number Line Approach
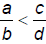 if and only if
if and only if
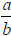 is to the left of
is to the left of
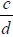 on the rational
number line.
on the rational
number line.
Addition Approach
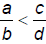 if and only if there is a positive rational
number
if and only if there is a positive rational
number 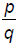 such that
such that
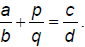
Cross-Multiplication of Rational-Number Inequality
Let 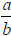 and
and
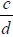 be any rational
numbers, where b > 0 and d > 0. Then
be any rational
numbers, where b > 0 and d > 0. Then 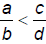 if and
if and
only if ad < bc.