Example 11. Complete the square to place f(x) =
2x2 + 4x − 4 in vertex form
and sketch its graph.
In the last two examples , we gained some measure of
success when the coefficient
of x2 was a 1. We were just getting comfortable with that situation and we’d
like
to continue to be comfortable, so let’s start by factoring a 2 from each term on
the
right-hand side of the equation .
f(x) = 2[x2 + 2x − 2]
If we ignore the factor of 2 out front, the coefficient of x2 in the trinomial
expression
inside the parentheses is a 1. Ah, familiar ground! We will proceed as we did
before,
but we will carry the factor of 2 outside the parentheses in each step . Start by
taking
half of the coefficient of x and squaring the result ; i.e., [(1/2)(2)]2 = 1.
Add and subtract this amount inside the parentheses so as
to not change the equation .
f(x) = 2[x2 + 2x + 1 − 1 − 2]
Group the first three terms inside the parentheses and combine constants.
f(x) = 2[(x2 + 2x + 1) − 3]
The grouped terms inside the parentheses form a perfect square trinomial that is
easily
factored.
f(x) = 2[(x + 1)2 − 3]
Finally, redistribute the 2.
f(x) = 2(x + 1)2 − 6
This is a parabola that opens upward. In addition, it is
stretched by a factor of
2, so it will be somewhat narrower than our previous examples . The parabola is
also
shifted 1 unit to the left, then 6 units downward, placing the vertex at
(−1,−6), as
shown in Figure 3(a). The table in Figure 3(b) calculates two points to the
right of
the axis of symmetry, and mirror points on the left of the axis of symmetry make
for
an accurate plot of the parabola.
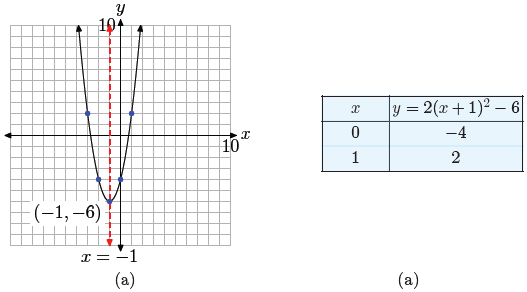
Figure 3. Plotting the graph of the
quadratic function f(x) = 2x2 + 4x − 4.
Let’s look at an example where the coefficient of x2 is
negative.
Example 12. Complete the square to place f(x) =
−x2 + 6x − 2 in vertex form
and sketch its graph.
In the last example, we factored out the coefficient of
x2. This left us with a
trinomial having leading coefficient 1, which enabled us to proceed much as we
did
before: halve the middle coefficient and square, add and subtract this amount,
factor
the resulting perfect square trinomial. Since we were successful with this
technique in
the last example, let’s begin again by factoring out the leading coefficient, in
this case
a −1.
f(x) = −1[x2 − 6x + 2]
If we ignore the factor of −1 out front, the coefficient of x2 in the trinomial
expression
inside the parentheses is a 1. Again, familiar ground! We will proceed as we did
before,
but we will carry the factor of −1 outside the parentheses in each step. Start
by taking
half of the coefficient of x and squaring the result; i.e., [(1/2)(−6)]2 = 9.
Add and subtract this amount inside the parentheses so as
to not change the equation.
f(x) = −1[x2 − 6x + 9 − 9 + 2]
Group the first three terms inside the parentheses and combine constants.
f(x) = −1[(x2 − 6x + 9) − 7]
The grouped terms inside the parentheses form a perfect square trinomial that is
easily
factored.
f(x) = −1[(x − 3)2 − 7]
Finally, redistribute the −1.
f(x) = −(x − 3)2 + 7
This is a parabola that opens downward. The parabola is
also shifted 3 units to
the right, then 7 units upward, placing the vertex at (3, 7), as shown in Figure
4(a).
The table in Figure 4(b) calculates two points to the right of the axis of
symmetry,
and mirror points on the left of the axis of symmetry make for an accurate plot
of the
parabola.
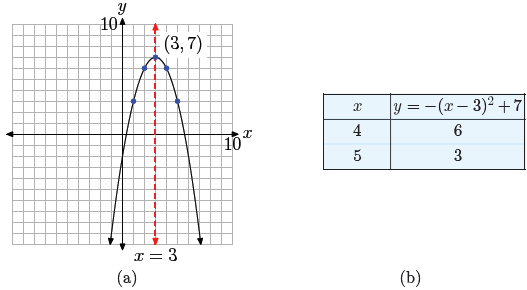
Figure 4. Plotting the graph of the
quadratic function f(x) = −(x − 3)2 + 7.
Let’s try one more example.
Example 13. Complete the square to place f(x) =
3x2 + 4x − 8 in vertex form
and sketch its graph.
Let’s begin again by factoring out the leading
coefficient, in this case a 3.
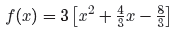
Fractions add a degree of difficulty, but, if you follow
the same routine as in the previous
examples, you should be able to get the needed result. Take half of the
coefficient of x
and square the result; i.e., [(1/2)(4/3)]2 = [2/3]2 = 4/9.
Add and subtract this amount inside the parentheses so as
to not change the equation.
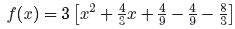
Group the first three terms inside the parentheses. You’ll
need a common denominator
to combine constants.
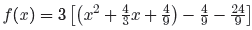
The grouped terms inside the parentheses form a perfect
square trinomial that is easily
factored.
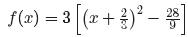
Finally, redistribute the 3.
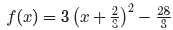
This is a parabola that opens upward. It is also stretched
by a factor of 3, so it
will be narrower than all of our previous examples. The parabola is also shifted
2/3
units to the left, then 28/3 units downward, placing the vertex at (−2/3,−28/3),
as
shown in Figure 5(a). The table in Figure 5(b) calculates two points to the
right of
the axis of symmetry, and mirror points on the left of the axis of symmetry make
for
an accurate plot of the parabola.
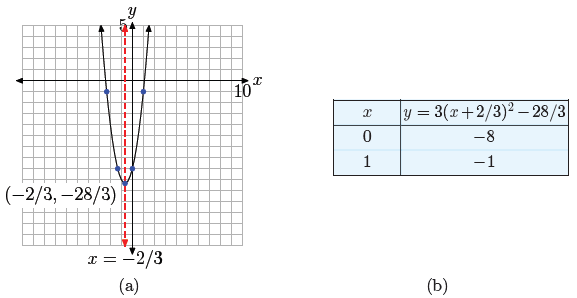
Figure 5. Plotting the graph of the quadratic
function f(x) = 3(x + 2/3)2 − 28/3.
