19.0: Students know the quadratic formula and are familiar
with its proof by
completing the square. |
a. Given a quadratic equation of the form: ax2 + bx + c =
0, a ≠ 0
What is the formula for finding the solutions to the equation ?
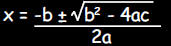
b. The equations below are part of a derivation of the
quadratic
formula by completing the square:
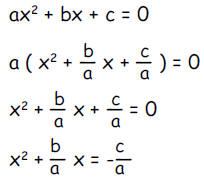
Which of the following is the best next step for the
derivation of the quadratic formula?
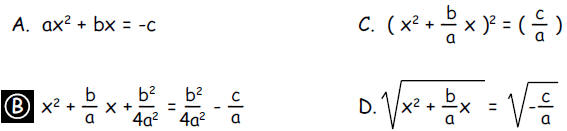
The derivation of the quadratic formula by completing the square is
standard material in any good Algebra I textbook. |
20.0: Students use the quadratic formula to find the roots
of a second-degree
polynomial and to solve quadratic equations. |
Find all values of x which satisfy the equation 4x2 - 4x -
1 = 0
| 21.0: Students graph quadratic functions and know that
their roots are the x-intercepts. |
You may assume that the following equation is correct for
all values
of x:
a. For which values of x, if any, does the graph of the
equation
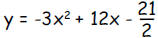 cross the x axis?
cross the x axis?
b. Sketch the graph of the equation
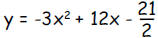
22.0: Students use the quadratic formula or factoring
techniques or both to determine
whether the graph of quadratic function will intersect the x-axis in zero, one
or two points. |
Use the quadratic formula or the method of factoring to
determine whether the
graphs of the following functions intersect the x axis in zero, one, or two
points.
(Do not graph the functions.)

23.0: Students apply quadratic equations to physical
problems, such as the motion of an
object under the force of gravity. |
a. If an object is thrown vertically with an initial
velocity of 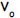 from
from
an initial height of 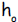 feet, then neglecting air friction its
feet, then neglecting air friction its
height h(t) in feet above the ground t seconds after the ball was
thrown is given by the formula
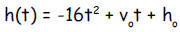
If a ball is thrown upward from the top of a 144 foot
tower at 96 feet per
second, how long will it take for the ball to reach the ground if there is no
air
friction and the path of the ball is unimpeded?
Let h(t) be the height above the ground at time t measured in seconds.
Then
h(t) - 16t2 + 96t + 144
In order to find t such that h(t) is zero, set h(t) = 0 and solve for t.
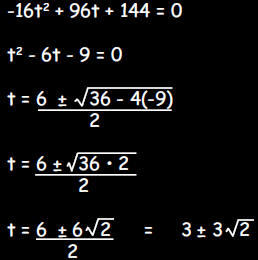
Since the object was thrown at t = 0 and time
moves forward, the correct
solution is 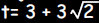 seconds. seconds. |
b. The boiling point of water depends on air pressure and
air pressure
decreases with altitude. Suppose that the height H above the
ground in meters can be deduced from the temperature T at which
water boils in degress Celsius by the following formula:
H = 1000(100 - T) + 580(100 - T)2
1. If water on the top of a mountain boils at 99.5 degrees Celsius,
how high is the mountain?

2. What is the approximate boiling point of water at
sea-level (H=0 meters)
according to this equation? Round your answers to the nearest 10 degrees.
The temperature at which water boils at sea level according to the
formula
may be deduced by setting H = 0 and solving for T:

The equation predicts the boiling point is
approximately 100°C |
24.0: Students use and know simple aspects of a logical
argument:
24.1: Students explain the difference between inductive and deductive reasoning
and provide
examples of each.
24.2: Students identify the hypothesis and conclusion in a logical deducation.
24.3: Students use counterexamples to show that an assertion is false and
recognize that a single
counterexample is sufficient to refute an assertion. |
a. Verify to your own satisfaction, by direct calculation,
the
correctness of the following equations (do not submit your
calculations on this exam):
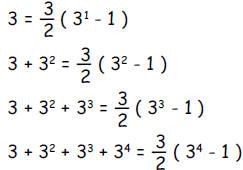
1. Using inductive reasoning, propose a formula that gives
the sum
for 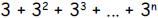 for any counting number n .
for any counting number n .
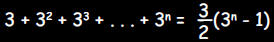
2. Does the sequence of formulas above prove that your
answer to part 1 is
correct? Explain your answer.
No, inductive reasoning is really a form of guessing based on previous
observations.
[Note to the reader: In this case the formula given in part 1 is correct
for any value of n. Inductive reasoning worked in this case, but it
doesn't always give correct answers.] |
b. Consider the following mathematical statement :
If y is a positive integer, then 1 + 1141y2 is not a perfect square.
1. Write the hypothesis of this statement.
2. Write the conclusion of this statement.
|
1 + 1141y2 is not a perfect square |
3. Use whole number arithmetic to prove that the conclusion is
correct when y = 1.
If y = 1, 1 + 1141y2 = 1142. To show that 1142 is not a perfect
square, it suffices to show that 1142 falls between the
squares of two consecutive integers.
332 = 1089 < 1142 < 1156 = 342
Therefore the conclusion, 1 + 1141y2 is not a perfect square, is
correct when y = 1. |
4. It has been shown by mathematicians that the conclusion
is correct for
each positive integer y up to and including 30,693,385,322,765,657,197,397,207.
However, if this number is increased by 1 so that
y = 30,693,385,322,765,657,197,397,208
then the positive square root of 1 + 1141y2 is
1,036,782,394,157,223,963,237,125,215
Is the statement, "If y is a positive integer, then 1 + 1141y2
is not a perfect square" correct? Explain your answer.
No, the statement is incorrect because the conclusion is
false for at least one positive integer value of y.
[Note that inductive reasoning for this problem would
most likely lead to a faulty conclusion.] |
25.0: Students use properties of the number system to
judge the validity of results,
to justify each step of a procedure, and to prove or disprove statements:
25.1: Students use properties of numbers to construct simple, valid arguments
(direct and
indirect) for, or formulate counterexamples to, claimed assertions.
25.2: Students judge the validity of an argument according to whether the
properties of the
real number system and the order of operations have been applied correctly at
each step.
25.3: Given a specific algebraic statement involving linear, quadratic, or
absolute value
expressions or equations or inequalities , students determine whether the
statement is true
sometimes, always, or never. |
a. Prove, using basic properties of algebra, or disprove
by finding a
counterexample, each of the following statements:
1. The set of even numbers is closed under addition .
A number m is even if and only if m = 2k for some integer k. Let m and n
be even and let m = 2k and m = 2j for integers k and j. Then:
m + n = 2k + 2j = 2(k + j)
Therefore m + n has a factor of 2 so it is even. This proves that the
sum
of any two even numbers is even and therefore the set of even numbers
is closed under addition. |
2. The sum of any two odd numbers is even.
A number m is odd if and only if m = 2k + 1 for some integer k. Let m
and n
be odd and let m = 2k +1 and n = 2j + 1 for integers k and j. Then:
m + n = (2k + 1) + (2j + 1) = 2k + 2j + 2 = 2(k + j + 1)
Therefore m + n has a factor of 2 so it is even. This proves that the
sum
of any two odd numbers is odd. |
a.
3. For any positive real number 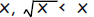
This statement is false. 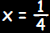 gives a
counterexample because: gives a
counterexample because:
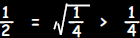 |
b. Find all possible pairs of numbers a and b which
satisfy the
equation a2 + b2 = (a + b)2. Explain your reasoning.
Suppose a2 + b2 = (a + b)2
Then a2 + b2 = a2 + 2ab + b2
Therefore 0 = 2ab
Therefore ab = 0
Therefore a = 0 or b = 0.
If a = 0 or b = 0 then a2 + b2 = (a + b)2.
We conclude that a2 + b2 = (a + b)2 if and only if a = 0 or b = 0 |
c. Identify the step below in which a fallacy occurs:
Step 1: Let a = b = 1
Step 2: a2 = ab
Step 3: a2 - b2 = ab - b2
Step 4: (a - b)(a + b) = b(a - b)
Step 5: a + b = b
Step 6: 2 = 1
Answer: Step 5
Explain why the step you have chosen as the fallacy is incorrect
Step 5 results from dividing both sides of the previous equation by
zero because a - b = 0. |
d. Is the following equation true for some values of x, no
values of x or all values
of x?
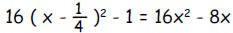
The equation is true for all values of x because for any
value of x:
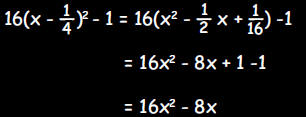 |



