In this lesson, students use their knowledge of exponents ,
roots , and area to prove the
Pythagorean theorem. Students work with numbers , pictures and algebraic symbols
to
understand this result. They use the Pythagorean theorem and its converse to
solve
problems.
This lesson falls near the end of a cluster of lessons
that apply algebra readiness concepts
of length, area, and volume. In earlier lessons, students found perimeters and
areas of
circles and rectangles , and they found surface areas and volumes of prisms and
cylinders.
They also established formulas for triangles and parallelograms using dissection
proofs. In
the last geometry lesson they will continue to use the Pythagorean theorem and
its converse
to solve problems .
Math Goals
• Explore the Pythagorean theorem numerically, algebraically, and
geometrically
• Understand a proof of the Pythagorean theorem
• Use the Pythagorean theorem and its converse to solve problems.
Abridged
California
Standards |
Algebra Readiness
• AF 1.1 Use variables and appropriate operations to write an expression
or an equation that
represents a verbal description
• MG 3.3 Know and understand the Pythagorean theorem and its converse
and use it to
find the length of the missing side of a right triangle and the lengths
of other line segments
and, in some situations, empirically verify the Pythagorean theorem by
direct measurement.General Mathematics
• MG2.1 Use formulas routinely for finding the perimeter and area of
basic two dimensional
figures, including rectangles, squares, and triangles. |
Summative
Assessment |
• Week 26 The Pythagorean Theorem (MG
3.3) |
PLANNING INFORMATION
| Estimated Time: 75 - 90 Minutes |
| Student Pages |
Overhead Transparencies |
Reproducibles |
SP1: Ready, Set, Go
SP2: Two Right Triangles
SP3-4: Pythagorean Theorem
(Part 1)
SP5: Pythagorean Theorem
(Part 2)
SP6-7: Pythagorean Theorem
Practice |
OH1: Ready, Set, Go
OH2: Two Right Triangles
OH3: Right Triangle ABC |
R1 Pythagorean Theorem Cut
Ups this will be the two
squares from SP3. I think two
sets of squares will fit on one
page. |
| Materials |
Prepare Ahead |
Management Reminders |
Rulers
Scissors
Calculators (optional)
Envelopes (optional) |
Make two squares from R1
into overheads and cut them
for demonstration. |
To save some class time, precut
R1 into large squares. |
| Homework |
Assessment |
Strategies for Special Needs |
Pythagorean Theorem
Practice (SP6) |
SPx: Knowledge Check
A1: Formative Quiz |
Manipulating polygons creates
a visual explanation for the
simplification of the
expressions 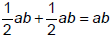
and 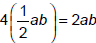 |
THE WORD BANK
A right triangle has exactly one right angle. The longest
side of a right triangle is called its
hypotenuse. The hypotenuse is opposite the right angle. The other two sides are
called
legs. The legs are both shorter than the hypotenuse, and they form the sides of
the right
angle.
The Pythagorean theorem states that, for a right triangle,
the sum of the squares of the
lengths of the legs is equal to the square of the length of the hypotenuse.
MATH BACKGROUND
| DOES a2 + b2 = c2 ? |
Math Background 1
Summarize 1,
Summarize 2 |
Caution: The slogan “a squared plus b
squared equals c squared” is an incomplete
statement of the Pythagorean theorem because there is no reference to a
right triangle nor
identification of the meaning of the variables. Here are preferred
statements:
1. For a right triangle, the sum of the
squares on the legs is equal to the square on the
hypotenuse. (A geometric focus: illustrated in the “Two Triangles”
exercise)
2. For a right triangle, the sum of the squares of
the lengths of the legs is equal to the
square of the length of the hypotenuse. (A numerical focus : derived in
the right triangle
cut-up proof)
3. For a right triangle with legs of length a and
b and hypotenuse of length c, a squared
plus b squared equals c squared. (More precise restatement of the
slogan) |
| ANOTHER PROOF OF THE
PYTHAGOREAN THEOREM |
Math Background 2
Extend |
The proof in this lesson is only one
of more than 400 proofs that have been recorded on
this famous theorem. Many are simple variations of each other.
Here is another proof, discovered in 1876 by President James A. Garfield
while a member
of the House of Representatives. Garfield was also a mathematics
teacher. cary, please
make diagram smaller
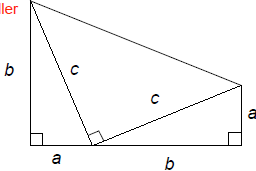
Let A be the area of the entire figure, which is a trapezoid. The area
of the trapezoid is:
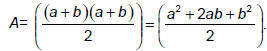
Area A can also be dissected into three triangles:
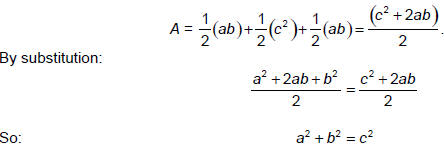 |



