I Taylor series approximation [25 points]
1. [5 points] If you are given a function f(x) and you seek its nth order Taylor
series approximation
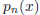[and remainder
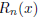] around 
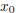and in the interval [a, b], how do you go about doing this?
Qualitatively, explain what conditions you think the function f(x) should
satisfy and the different
forms of the remainder at your disposal. Do you think there is a relationship
between the two forms
of remainder?
[2 points] for the first part if you give the formulation of Taylor series and
the remainder.
[1 point] for the conditions. It is important to state that f(x) as well as its
n derivatives are contin-
uou and differentiable over [a, b]. For most of you I took off 0.5 points if you didn't talk about the
differentiabilty of the derivatives.
[1 point] different forms of remainder: Cauchy form and the Lagrange form. Also
give the mathematical
form. Just stating the names is not sufficient.
[1 point] The relationship is that both are equivalent and one can be derived
from the other using the
Integral Mean Value theorem .
2. [5 points] Work out the second-order Taylor-series approximation
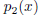for the function f(x) =
exp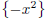 
at 
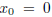and in the interval [a, b]. What is the remainder
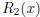? Write down the
condition that 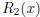must satisfy for
.
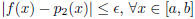[2 points] The taylor series expansion is: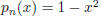 
[2 points] The remainder is: R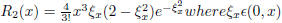
[1 point]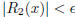
. For the condition to be satisfied
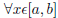, state that we need to find
.
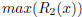Some people also solved it by using the series of ex and then replacing xin the
expansion with -x2 which
is perfectly okay. If I took off your points for doing this bring it back to me
and you "might" get your
points back.
3. [5 points] What is the first order Taylor series approximation
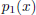for the
function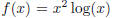 
[where log is the natural logarithm] in the interval [0, 1] and for x0 = 0?
[Hint: You'll have to take the
limits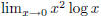 
and
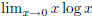and use the
form.] What is the remainder R1(x) and what
is its worst (largest absolute) value in the interval [0, 1]? What is the error
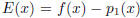? Is
there a discrepancy? Discuss.
[2 points]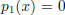 
: Note that here 
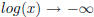as
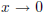.So you were required
to tale the limit of
the function at x=0 using the L'Hopital's rule.
[1 point]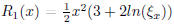 
[1 point] l R1(x) l is maximum w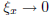hen
then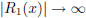 
[1 point] There is no discrepancy because the error
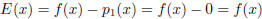:and hence
that the max abs remainder is infinite is perfectly okay.
4. [10 points] Given a function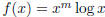
where m is
an arbitrary integer greater than zero, find the
order n for which the Taylor series approximation
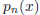at
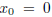is non-zero.
Is there a fundamental
problem with finding such a Taylor series approximation? Discuss.
[8 points] Keep differentiating and you will find that each derivative term of f (x)
contains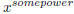 
term
and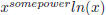 
term. So for the second term again we have to take the limit
at x = 0. Otherwise
there is this fundamental difficulty that f(x) becomes infinity at x = 0 [2
points].
Now take first derivative of x. We see that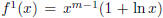 
. In this the
first term that is
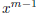will become non zero at x = 0 if we differentiate it m-1 times , i.e., we
have to have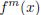 
which
means n = m and hence the number of terms in the taylor expansion = m+1.
II Derivative approximations [25 points overall]
1. [5 points] What is the fundamental goal of the derivative approximation?
Explain clearly the steps
involved in beginning with a function f(x) and ending up with a first derivative
approximation for the
function.
Almost everyone got 5 points.
2. [5 points] If you are given the Taylor series approximation
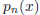for a
function f(x) at x0, how does this
change into an equivalent approximation for f(x + h) in terms of f(x)? Write
down the equivalences
between (x, x0) in 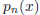and (x + h, x) in the approximation for f(x + h).
x is same as x+h and x0 is same as x.
3. [5 points] Is the approximation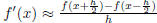 
a valid
first derivative approximation? [For a
derivative approximation to be valid,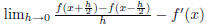 
should
equal zero.]
You have to evaluate the above limit and show that
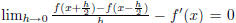.This can be
easily done by expanding the two taylor series for
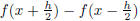and showing that the higher
order terms tend to zero as x tends to zero.
4. [10 points] Begin with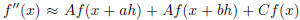 
. Construct an
approximation to
f''(x) by ensuring that i) the term involving f(x) is zero, ii) the term
involving f'(x) is zero, and iii)
that the coefficient of f ''(x) is one. Write down the resulting constraints
involving A, C, a, b, and h.
Pick a set of possible values for (A, C, a. b) that satisfy the constraints.
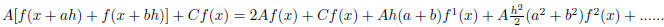
Applying the conditions we get
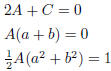
choose A = 1,C = -2,a = 1and b = -1. Now our A and C in the above equations
are different than
those in the question. So A = 1/h2 and C = -2/h2
III Linear Interpolation and Trapezoid Rule [25 points overall]
1. [5 points] What is the relationship between the linear interpolation of a
function f(x) in the interval
[a, b] and the trapezoid rule. Conceptually relate the two.
The trapezoid rule approximates the integral of the function by integrating over
the linear interpolant
of the function rather than the actual function itself.
2. [5 points] Construct a linear interpolation for f(x) = sin(x) for
. What is the worst case error
for this linear interpolation if you use the error bound?
The worst case error is:
3. [5 points] Construct a trapezoidal rule integration of
.
The trapezoid rule integration is the area under the linear interpolant:
So,
4. [10 points] Given four points A = (1, 5), B, C and D = (2, 3) and the linear
interpolation between B
and C to be 3x + 4y = 5 can you find the coordinates for B and C if you also know
that the slope of
the line joining A and B is 0.5 and that the slope of the line joining C and D
is 2. (This kind of a
problem arises in the spline literature.) Note that we know the equation of the
line between B and C.
[If you have difficulty solving simultaneous equations, just write down the
conditions satisfied by the
points B and C and you'll get a lot of partial credit.]
Find the equation of AB:
y = 0.5x + c1This will satisfy point A(1,5). So,
5 = 0.5 *1 + c1So, c1 = 4.5.
Hence, AB: y = 0.5x + 4.5
Similarly find CD:
y = 2x + c2 This satisfies point D(2,3). So,
3 = 2 *2 + c2 So, c2 = -1
Hence, CD: y = 2x - 1
Now you get B by solving AB and BC. And you get C by solving BC and CD. the
equation of BC is
given to be : 3x + 4y = 5
It is uptill this point that you get 9/10 points. This is also what was
mentioned in the question that
if you have difficulty solving simultaneous equations then you can leave upto here
and you get a lot of
partial credit. If you also solve further then you get 10/10.
IV. Newton's method [25 points overall]
1. [5 points] Give a conceptual level explanation of Newton's method. Pick a
function f(x) and clearly
explain what it is that the algorithm is trying to achieve.
see the textbook.
2. [5 points] Apply Newton's method to find the root at the origin for the
function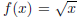 
with an
initial condition x0 > 0. Does the process converge?
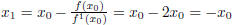: The process does not converge. Note that it
is also not oscillatory
because -x0 because x0 > 0 is negative and does not lie in the domain making
f(x) imaginary there.
If you do not specify this or write it to be oscillatory instead you lose 2
points.
3. [5 points] Given a function g(x) which is continuous and twice differentiable
in the interval (-∞,∞),
use Newton's method to find the location α where the function attains its minimum.
[You may assume
if you wish that the function has only one minimum occurring at x = 0.]
The Newton's method finds the roots of the equation. Now a function g(x) attains
minima when
g1(x) = 0. So, here we have to apply Newton's method on g1(x) and not g(x).
So, Newton's method will be:
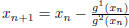
4. [10 points] Sketch a function that satisfies the following properties. i) The
function f(x) is continuous
and differentiable in (-∞,∞), ii) the function f(x) = 0 at x = 0, iii)
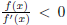for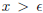 
where
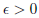can be made arbitrarily small, iv) 
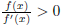for
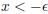. What happens when you run Newton's
method on such a function? Qualitatively explain the different scenarios that
unfold for different initial
conditions x0.
See the scanned image that I will post tonight.
