1 Finding Roots 8.1
By the end of this section, you should be able to solve
the following problems.
1. Find the principal square root of the given number.
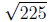
2. Find the value of the radical .
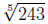
3. Identify the number as rational , irrational, or
non-real.
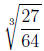
4. Mario is flying a kite with a string of 80 ft. The
horizontal distance
between Mario and the kite is 35 ft. How high is the kite above the
ground if Mario’s hands are 4 feet above the ground? Approximate the
answer to the thousandths place.
2 Concepts
The square root of a number simply asks the question,
“What factor when
used twice gives that number back”. The cube root of a number asks, “What
number when used as a factor 3 times gives that number back.” Therefore, for
any n, the nth root of a number asks, “What number when used as a factor
n times will give that number back.” Some simple examples will illustrate.
2.1 Examples
1. The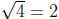
because 2 · 2 = 4
2. The
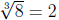because 2 · 2 · 2 = 8
3. The
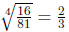because
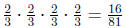
3 Concepts
There are a few other facts to notice about finding roots. The first is that
we are always solving the equation x n = a, and, in particular, when we
are solving x2 = a, a could be either positive or negative. For example,
in the statement
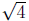could have root +2 or −2 because (+2)(+2) = 4 or
(−2)(−2) = 4. So for the solution to x 2 = a, we write
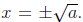An even
more technical reason for this comes from the definition of absolute value.
Absolute value is defined as the square root of a squared number. That is,
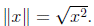Therefore,
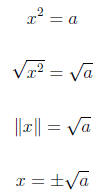
Aside from what a principal square root is, we must also understand that it
is not possible to take an even root of a negative number . For example, the
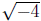does not exist in the real number system because no number when used
a factor twice will give a negative product . Therefore, we say the solution of
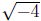is not real. In general,
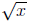is only true for x ≥ 0 In our next example, we
use our ability to find square roots to solve an application of the Pythagorean
Theorem.
3.1 Example
A tetherball pole cast a shadow 5ft long at a particular time of the day. If
the tetherball pole is 12ft high, find the distance between the top of the pole
and the tip of its shadow. Below is a picture of this situation.
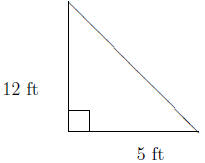
We can assume that the pole makes a right angle with the ground because
otherwise the problem won’t work. Now that we imagine a right triangle,
we can apply the Pythagorean Theorem. The a and b in the formula below
designate the legs that meet at right angles. c always designates the longest
side of the right angle which is the side opposite the right angle. It is called
the hypotenuse.
We now state the Pythagorean Theorem
a2 + b2 = c2
Substituting we have :
(12)2 + (5)2 = c2
144 + 25 = c2
169 = c2
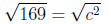
13 = c
Notice, we take principal square root here because it is an applied problem
4 Facts
1. We take the positive square root of a number to be the principal square
root. That is, the principle square root of
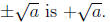
2. Any even root of a negative number will not be real.
3. The square root of any prime number is always irrational. Irrationals
can not be written in ratio form a/b (b ≠ 0).
4. Any real number that is not irrational is rational.
5. In the Pythagorean Theorem, the legs a and b meet at right angles,
and the longest side c, is opposite the right angle. The formula for the
Pythagorean Theorem is stated below
a2 + b2 = c2
5 Exercises
1. Find the principal square root of the given number.
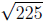
2. Find the value of the radical
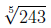
3. Identify the number as rational, irrational, or non-real.
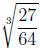
4. Mario is flying a kite with a string of 80 feet. The horizontal distance
between Mario and the kite is 35ft. How high is the kite above the
ground if Mario’s hands are 4 feet above the ground? Approximate the
answer to the thousandths place
6 Solutions
1. Find the principal square root of the given number.
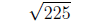
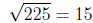
2. Find the value of the radical
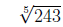
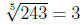
because
3 · 3 · 3 · 3 · 3 = 243
3. Identify the number as rational, irrational, or non-real.
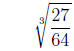
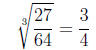
which is a rational number.
4. Mario is flying a kite with a string of 80 feet. The horizontal distance
between Mario and the kite is 35ft. How high is the kite above the
ground if Mario’s hands are 4 feet above the ground? Approximate the
answer to the thousandths place.
(35)2 + x2 = (80)2
1225 + x2 = 6400
−1225 − 1225
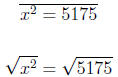
x ≈ 71.937
x + 4 ≈ 75.937
