Solve the equation 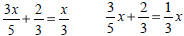
Find the common denominator and multiply both sides of the
equation by it.

Solve the equation 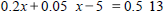
Find the common denominator and multiply both sides of the
equation by it.
The formula W= 0.3x + 46.6 models the average
number of hours worked by
American workers per week when W is the hours worked and x is the number
of
years since 1980. When will we average 55 hours per week?
The average American is probably working 55 hours per week
now, 28 years after 1980.
Einstein’s formula E = mc2, relates energy
and mass with the speed of light. E
represents energy in ergs, m represents
mass in grams, and c is the speed of light in
centimeters per second. The speed of light
in a vacuum is 3 × 1010 meters per second.
The square of 3 × 1010 is 9 × 1020 . 1 gram
of matter will contain 9 × 1020 ergs of
energy. The energy in 1 gram of matter
could move another gram of matter
559,234,073,013,000 miles at a rate of 1
centimeter per second. |
 |
Solve the equation E = mc2 for m.
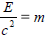
Solve the equation E = mc2 for c2.
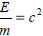
P= 2l+2w is the formula for calculating the perimeter of a
rectangle. l represents the length of a side of the rectangle and
w represents the width.

Solve P= 2l+2wfor w.
Add 2 to both sides
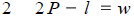
Multiply both sides by
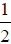
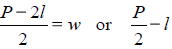
|
Solve the equation
3x + 7y = 21 for x |
Solve the equation
3x + 7y = 21 for y |
| |
|
|
Subtract
7y from both sides |
Subtract
3x from both sides |
| |
|
|
3x + 7y – 7y = 21 – 7y |
3x – 3x + 7y = 21 – 3x |
| |
|
|
3x = 21 – 7y |
7y = 21 – 3x |
| |
|
|
Divide both sides by 3 |
Divide both sides by 7 |
| |
|
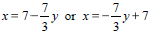 |
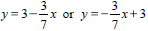 |
The distance a car will travel is calculated with the
formula d= rt,
where d is the distance traveled, r is the rate of travel and t
is the
time traveling.
How far will the car travel at a rate of 75 miles per hour in 3
hours?

How long will the it take the car to travel 175 miles at a
rate of 75
miles per hour?
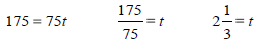
How fast was the car traveling if it went 390 miles in 5
hours?
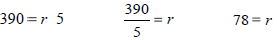
|
Solve the equation
3x+ 6 = 3(x+ 5) |
Solve the equation
-2x+ 5x–18 = -3x + 6(x–3) |
| |
|
|
Distribute |
Distribute |
| |
|
|
3x+ 6 = 3x+ 15 |
–2x+ 5x–18 = –3x + 6x–18 |
| |
|
|
Subtract3xfrom both sides |
Combine like terms |
| |
|
|
6 = 15 |
3x–18 = 3x –18 |
This is never true. There is no
solution . This is a contradiction. |
This is always true. There are infinitely
many solutions . This is an identity. |



