6 Roots of 1
The next place where this wonderful formula comes in handy is that it will help
us to find all of the n-th roots of any complex number . We will start by finding
all of the n-th roots of 1.
Finding the n-th roots of 1 means solving the equation
xn = 1 or, rewriting: xn - 1 = 0:
We expect there to be n roots since this is a degree n polynomial equation .
How shall we get at them, though? Let's try a few easy examples.
n = 1: There is only 1 1st root of 1, namely 1. This has length 1 and can be
written as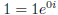 
; that is, r = 1 and θ = 0.
n = 2: There are two square roots of 1: 1 and -1. These can be written as
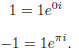
n = 3: We want to solve x 3-1 = 0, and we know
that 1 is one of the solutions.
In fact,
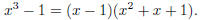
Using the quadratic formula on the second factor yields the roots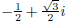
and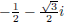
. These roots can be written as
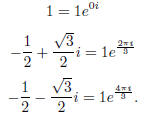
n = 4: We want to solve x 4 - 1 = 0. We can
factor as follows:
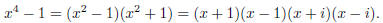
The four roots are therefore 1, -1, i, and -i. These roots
can be written as
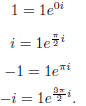
n = 5: Too hard for us at the moment...
Now, let's plot these complex numbers to find a pattern.
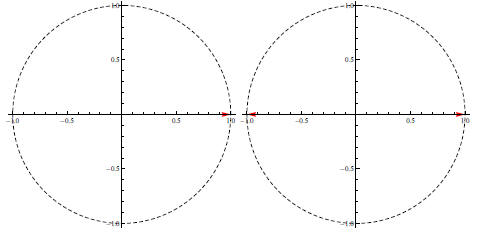
Figure 3: Left: 1st root of 1. Right: 2nd roots of 1
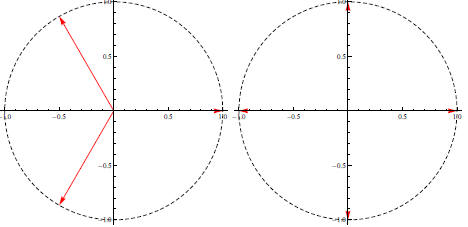
Figure 4: Left: 3rd roots of 1. Right: 4th roots of 1
Notice that the n roots are equally spaced around the unit
circle in each
case . To be specific, we have the following principle: The nth roots of 1 are
given by
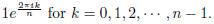
For n = 5, we get the following roots of 1:
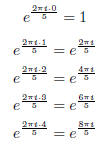
7 nth Roots of any Complex Number
Let's assume we have a complex number in polar form
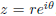. It is actually
very easy to get one nth root:
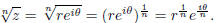
What about the other roots? Those can be found by
multiplying the one
root by all nth roots of 1.
Example: Find all six of the sixth roots of 64i.
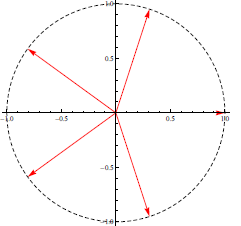
Figure 5: 5th roots of 1
Solution : Start by converting to polar form:
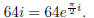
Now find a sixth root of i:
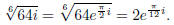
Next, find all of the sixth roots of 1:
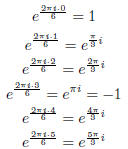
Finally, take the sixth root of i and multiply it be each
of the sixth roots of
1:
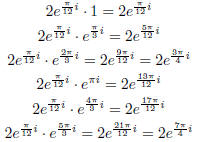
A motivated student might convert the third and sixth to
rectangular co-
ordintes. Once more, let's look at the geometry of the situation:
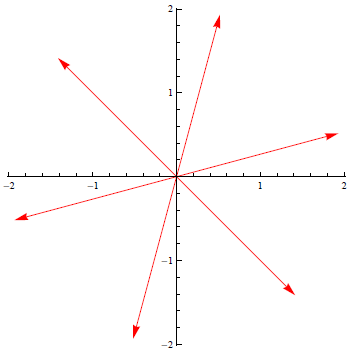
Figure 6: 6th roots of i
