DISTANCE, CIRCLES, AND QUADRATIC EQUATIONS

EXERCISE SET G

1. Where in this section did we use the fact that the same scale
was used on both coordinate axes ?
2–5 Find
(a) the distance between A and B
(b) the midpoint of the line segment joining A and B.

2. A(2, 5), B(−1, 1)
3. A(7, 1), B(1, 9)
4. A(2, 0), B(−3, 6)
5. A(−2,−6), B(−7,−4)

6–10 Use the distance formula to solve the given problem.

6. Prove that (1, 1), (−2,−8), and (4, 10) lie on a straight line.
7. Prove that the triangle with vertices (5,−2), (6, 5), (2, 2)
is isosceles.
8. Prove that (1, 3), (4, 2), and (−2,−6) are vertices of a right
triangle and then specify the vertex at which the right angle
occurs.
9. Prove that (0,−2), (−4, 8), and (3, 1) lie on a circle with
center (−2, 3).
10. Prove that for all values of t the point (t, 2t − 6) is equidistant
from (0, 4) and (8, 0).
11. Find k, given that (2, k) is equidistant from (3, 7) and (9, 1).
12. Find x and y if (4,−5) is the midpoint of the line segment
joining (−3, 2) and (x, y).

13–14 Find an equation of the given line.

13. The line is the perpendicular bisector of the line segment
joining (2, 8) and (−4, 6).
14. The line is the perpendicular bisector of the line segment
joining (5,−1) and (4, 8).
15. Find the point on the line 4x − 2y + 3 = 0 that is equidistant
from (3, 3) and (7,−3). [Hint: First find an equation of
the line that is the perpendicular bisector of the line segment
joining (3, 3) and (7,−3).]
16. Find the distance from the point (3,−2) to the line
(a) y = 4 (b) x = −1.
17. Find the distance from (2, 1) to the line 4x − 3y + 10 = 0.
[Hint: Find the foot of the perpendicular dropped from the
point to the line.]
18. Find the distance from (8, 4) to the line 5x + 12y − 36 = 0.
[Hint: See the hint in Exercise 17.]
19. Use the method described in Exercise 17 to prove that the
distance d from (x₀, y₀) to the line Ax + By + C = 0 is

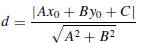
20. Use the formula in Exercise 19 to solve Exercise 17.
21. Use the formula in Exercise 19 to solve Exercise 18.
22. Prove: For any triangle, the perpendicular bisectors of the
sides meet at a point. [Hint: Position the triangle with one
vertex on the y-axis and the opposite side on the x-axis, so
that the vertices are (0, a), (b, 0), and (c, 0).]

23–24 Find the center and radius of each circle.

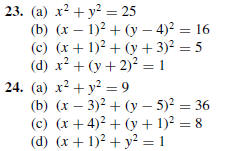
25–32 Find the standard equation of the circle satisfying the
given conditions.

25. Center (3,−2); radius = 4.
26. Center (1, 0); diameter =
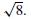
27. Center (−4, 8); circle is tangent to the x-axis.
28. Center (5, 8); circle is tangent to the y-axis.
29. Center (−3,−4); circle passes through the origin.
30. Center (4,−5); circle passes through (1, 3).
31. A diameter has endpoints (2, 0) and (0, 2).
32. A diameter has endpoints (6, 1) and (−2, 3).

33–44 Determine whether the equation represents a circle,
a point, or no graph. If the equation represents a circle, find
the center and radius.

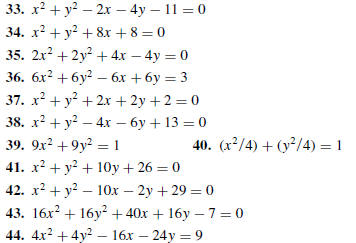
45. Find an equation of
(a) the bottom half of the circle x² + y² = 16
(b) the top half of the circle x² + y² + 2x − 4y + 1 = 0.

46. Find an equation of
(a) the right half of the circle x² + y² = 9
(b) the left half of the circle x² + y² − 4x + 3 = 0.

47. Graph

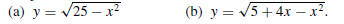
48. Graph

49. Find an equation of the line that is tangent to the circle

x² + y² = 25

the point (3, 4) on the circle.

50. Find an equation of the line that is tangent to the circle at
the point P on the circle
(a) x² + y² + 2x = 9; P(2,−1)
(b) x² + y² − 6x + 4y = 13; P(4, 3).

51. For the circle x² + y² = 20 and the point P(−1, 2):
(a) Is P inside, outside, or on the circle?
(b) Find the largest and smallest distances between P and
points on the circle.

52. Follow the directions of Exercise 51 for the circle
x² + y² − 2y − 4 = 0
and the point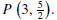

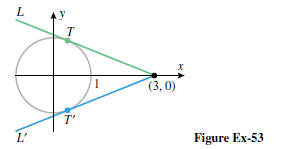
53. Referring to the accompanying figure, find the coordinates
of the points T and T', where the lines L and L' are tangent
to the circle of radius 1 with center at the origin.

54. Apoint (x, y) moves so that its distance to (2, 0) i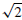s times
its distance to (0, 1).
(a) Show that the point moves along a circle.
(b) Find the center and radius.

55. A point (x, y) moves so that the sum of the squares of its
distances from (4, 1) and (2,−5) is 45.
(a) Show that the point moves along a circle.
(b) Find the center and radius.

56. Find all values of c for which the system of equations

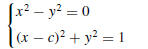
has 0, 1, 2, 3, or 4 solutions . [Hint: Sketch a graph.]

57–70 Graph the parabola and label the coordinates of the
vertex and the intersections with the coordinate axes.

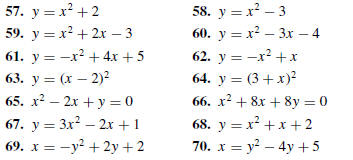
71. Find an equation of
(a) the right half of the parabola y = 3 − x²
(b) the left half of the parabola y = x² − 2x.

72. Find an equation of
(a) the upper half of the parabola x = y² − 5
(b) the lower half of the parabola x = y² − y − 2.

73. Graph

74. Graph

75. If a ball is thrown straight up with an initial velocity of
32 ft/s, then after t seconds the distance s above its starting
height, in feet, is given by s = 32t − 16t² .
(a) Graph this equation in a ts-coordinate system (t-axis
horizontal).
(b) At what time t will the ball be at its highest point, and
how high will it rise?

76. A rectangular field is to be enclosed with 500 ft of fencing
along three sides and by a straight stream on the fourth side.
Let x be the length of each side perpendicular to the stream,
and let y be the length of the side parallel to the stream.
(a) Express y in terms of x .
(b) Express the area A of the field in terms of x.
(c) What is the largest area that can be enclosed?

77. Arectangular plot of land is to be enclosed using two kinds
of fencing. Two opposite sides will have heavy-duty fencing
costing $3/ft, and the other two sides will have standard
fencing costing $2/ft. A total of $600 is available for the
fencing. Let x be the length of each side with the heavy-duty
fencing, and let y be the length of each side with the
standard fencing.
(a) Express y in terms of x.
(b) Find a formula for the area A of the rectangular plot in
terms of x.
(c) What is the largest area that can be enclosed?

78. (a) By completing the square, show that the quadratic equation
y = ax² + bx + c can be rewritten as

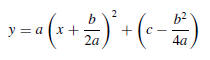
if a ≠ 0.

(b) Use the result in part (a) to show that the graph of the
quadratic equation y = ax² + bx + c has its high point
at x = −b/(2a) if a < 0 and its low point there if a > 0.

79–80 Solve the given inequality

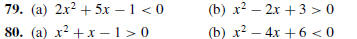
81. At time t = 0 a ball is thrown straight up from a height of 5
ft above the ground. After t seconds its distance s, in feet,
above the ground is given by s = 5 + 40t − 16t².
(a) Find the maximum height of the ball above the ground.
(b) Find, to the nearest tenth of a second, the time when the
ball strikes the ground.
(c) Find, to the nearest tenth of a second, how long the ball
will be more than 12 ft above the ground.

82. Find all values of x at which points on the parabola y = x²
lie below the line y = x + 3.