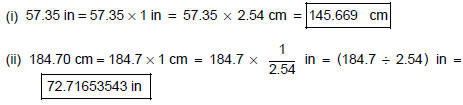1. (a) Estimate the product 43.7 × 3.8 by rounding
to whole Numbers.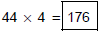
Note that we do not find the exact product and then round .
The estimate is not a
round-off of the exact product in (b), but can help confirm the placement of the
decimal.
(b) Compute the exact product 43.7 × 3.8 by
hand. Do not round.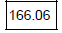
(c) Estimate the quotient 43.91 ÷ 11.3 by rounding
to whole numbers.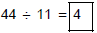 
(d) Compute the quotient 43.91 ÷ 11.3, without
rounding divisor or dividend,
by hand, rounding the quotient to two decimal places.
 |
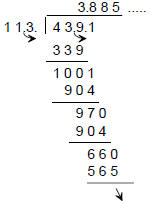Move the decimal in the divisor just far enough to the
right to make it an integer. (One place, here.)
Move the decimal in the dividend the same number of
places . Perform long division as usual. The decimal
in the quotient is placed directly above the new
decimal in the dividend. Continue until the digit after
the place where we are to round is obtained.
Rounding, we get  |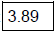
2. (a) A machine runs for 5 hr 52 min, then runs 4 hr 45
min more.
How much total time did the machine run? Answer with a sentence. (1 hr = 60 min)
5 hr 52 min + 4 hr 45 min = 9 hr 97 min = 9 hr + 60 min + 37 min = 10 hr 37 min
| The machine ran for a total of 10 hr 37 min. |
(b) There was 6 lb 10 oz of flour left in a bag. Of this
flour, 2 lb 12 oz is used
for a recipe. How much flour is now left in the bag? (1 lb = 16 oz)
6 lb 10 oz − (2 lb 12 oz) = 5 lb 26 oz − 2 lb − 12 oz = 3 lb 14 oz
| There are 3 lb 14 oz of flour left in the bag. |
3. Convert to reduced fractions .
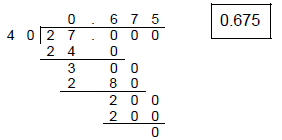
4. (a) Convert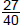 
to a
decimal, showing the long division setup. Do not round.
(b) Convert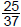 
to decimal
form using bar notation in the simplest way.
 |
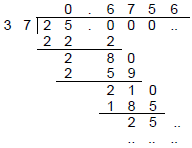The remainder of 25 has occurred before. (It’s the
original dividend, actually.) The process repeats
thereafter.
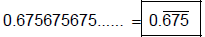
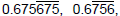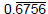Comments:  etc are unsimplified.
 and
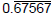 are incorrect. They are not
equal to the fraction 25/37. 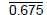 is bad
notation. |
c) Convert 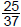to decimal
form, rounded to three decimal places.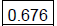 
We must know the digit in the fourth decimal place to round correctly.
5. Given the numbers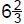 
and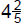 
, find the mixed number form of the
|
(a) sum |
 |
|
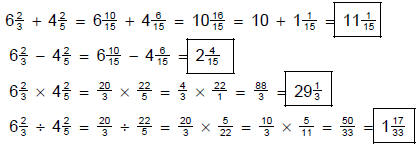(b) difference |
|
(c) product |
|
(d) quotient |
6. Simplify
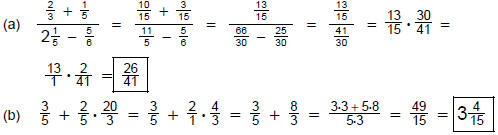
7 (a) Write 3,080,000,000,000 in scientific notation.
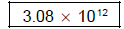
(b) Write 0.00000073 in scientific notation.
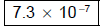
(c) Write 3.5 × 10-4 in standard decimal
notation.
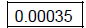
8. (a) If a lawn can be mowed in
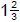hours, how long will it take to mow 9 lawns?
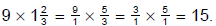
| It will take 15 hours to mow 9 lawns. |
(b) If a lawn can be mowed in
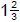hours, how many can be mowed in 10 hours?
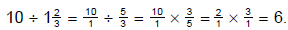
| Six lawns can be mowed in ten hours. |
9. Given the data 55, 50, 90, 44, 95, 75, 57, 82,
find
(a) the mean (to 3 decimal places)
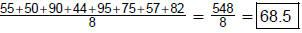
(b) the median Arrange lowest to highest. 44, 50,
55, 57, 75, 82, 90, 95.
The number of data is even. Find the mean of the middle two numbers in size.
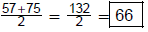
(c) the range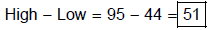 
10. (a) Check the proportion
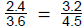, and state if it is true or false. The
product of
the extremes should equal the product of the means. 2.4 × 4.5 = 3.6 × 3.2,
10.8 = 11.52 is false. The proportion is false .
(b) Solve the proportion
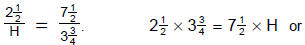
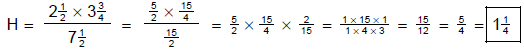
11. If we can drive 550 miles on 20 gallons of gas, how
far can we drive on
16 gallons of gas? Set up and solve a proportion to solve the problem. Answer
with a sentence.
Plan: 
Let the distance
be X Miles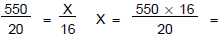 
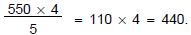Check:
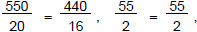true.
| We can drive 440 miles on 16 gallons of gas. |
12. Brand A gasoline cost $48 for 16 gallons. Brand B
gasoline cost $42 for 15 gallons.
Brand C gasoline cost $52 for 18 gallons. Compare unit ratios and decide which
is the
best buy, if the brands are equal in quality. Answer with a sentence.
Plan: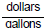
Fewer dollars per
gallon is better. Brand A: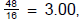
Brand B: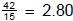 
, Brand C: .
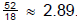2.8 < 2.89 < 3
(Be sure to keep enough decimal places when rounding to see the differences .)
13. (a) Simplify the ratio : 5 hr 36 min to 2 hr 33 min.
Convert to common units.
The ratio is 336 minutes to 153 minutes. Cancel the minutes and reduce .
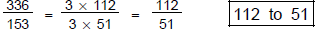
(b). Convert the units as indicated. Write down
your calculator display .
1 inch = 2.54 cm, 1 cm = 0.3937 inch
