On the Use of Computer Algebra Syntax in
the Calculus Classroom
Abstract
In this talk, the idea of using computer algebra syntax in
a
calculus course will be presented. The presenter believes that
students, to a certain degree, can become acquainted with
CAS conventions and syntax before ever sitting down and
wrestling with such software.
Moreover, this intentional syntactical use might lead to
better understanding of the composition of functions, and thus
better understanding of the concepts of the Chain Rule (for
derivatives) and the Substitution Method (for antiderivatives).
The presenter will show some sample assignments as well
as discuss the pros and cons of such an idea. There will be
time for general discussion of this notion both during the
presentation time, and hopefully afterwards for any interested
parties.
The Main Issues
• Student understanding of composition of
functions and order of operations
• The steep learning curve of Mathematica
(or any other CAS)
• Students' electronic communication of
mathematics (e.g. via email, on message
boards, etc.)
Ideas and Implementation
• Compare /contrast mathematical notation
and computer algebra syntax
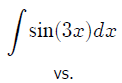
Integrate[Sin[3x],x]
• Occasional but consistent use of
Mathematica syntax in class
• Guidelines for electronic
communication of mathematics
• Any others?
Pros and Cons
• Cons
1. The Mathematica learning curve
2. Isn't calculus hard enough already?
• Pros
1. Fewer mathematically ambiguous
emails!
2. Students are forced to think about
composition of functions
3. Math/CS majors are introduced to
conventions of a programming
language
You may spend as much time on this exam as you wish, but
once you begin working on
it, you may not consult any resources (including calculators and Russ !) until
you have
completed it. Your exam will be graded before you leave.
Evaluate each antiderivative. SHOW ALL OF YOUR WORK!
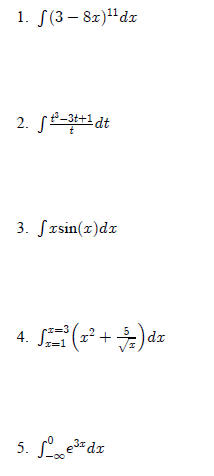
You may spend as much time on this exam as you wish, but
once you begin working on
it, you may not consult any resources (including calculators and Russ!) until
you have
completed it. Your exam will be graded before you leave.
Evaluate each antiderivative. SHOW ALL OF YOUR WORK!
1. Integrate[(3-8x)^11,x]
2. Integrate[(t^3-3t+1)/t,t]
3. Integrate[x*Sin[x],x]
4. Integrate[x^2+5/Sqrt[x],{x,1,3}]
5. Integrate[Exp[3x],{x,-Infinity,0}]
Guidelines for Mathematical Emails
In this course, I strongly encourage you to come to my
office hours for help with
homework or preparation for exams. However, the use of email as a form of
communication is also encouraged. The following is a list of “translations” of
mathematical notation into pure text format. I would encourage everyone to
become
familiar with these conventions and to use them in any mathematical email
correspondence with me.
-----Original Message-----
From: Andrew C Hartwig
Sent: Wednesday, February 12, 2003 5:10 PM
To: Russell Goodman
Subject: RE: YO Questions
Prof G
Can I legally move the five out front with
this expression
u^5 * ln 5u to
5 integral u^5 * ln u
Andy
-----Original Message-----
From: Russell Goodman
Sent: Fri 10/11/2002 8:38 AM
To: Sundance Visser
Subject: RE: calculus
Sunny:
***SNIP***
On #16, substitution does work. Let w = 5u,
so that dw = 5du AND u = (1/5)w. The
integral then becomes:
Integrate[(w/5)^5* Log [w]*(1/5),w]
=Integrate[(w^5/5^5)*(1/5)*Log[w],w]
=Integrate[(w^5/5^6)*Log[w],w]
=(1/5^6)*Integrate[w^5*Log[w],w]
It's a bit ugly, but I hope that helps!!
From: Russell Goodman
Sent: Tuesday, October 08, 2002 10:52 AM
To: Brady E Kurtz
Subject: RE: 7.2 homework questions
***SNIP***
Anyway... The derivative of (Log[t])^2
requires the Chain Rule:
D[Log[t]^2,t] = 2Log[t]*(1/t)
Now, if you meant problem #35 ( like others
have asked about), use the hint:
D[ArcSin[u^2],u] = 2u/Sqrt[1-u^4], where
Sqrt means square root .
***SNIP***
From: Russell Goodman
Sent: Wednesday, March 19, 2003 2:30 PM
Subject: [Calc 2] Mathematica Help
I realized a few minutes ago that
Mathematica's " Solve " command doesn't work
too well when using functions like Cosh[x],
so here's an alternative, if you need it.
If I were trying to solve the equation
15Cosh[45/x]-x^2=0, I would want to use the
following Mathematica command, called
"FindRoot":
FindRoot[15Cosh[45/x]-x^2 == 0, {x,20}]
The {x,20} part just tells Mathematica what
variable you 're using and it also gives it a
"starting x- value " to try, just like the
"Guess" that the TI-83 asks you for when
doing certain things. I just guessed x=20
to start off with.



