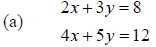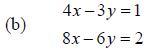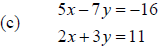I. Solving Systems of Linear Equations Graphically
1. Given the two functions and 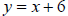 and
and
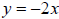 ,
,
(a) What are the slope and y - intercept of 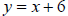 ?
?
slope:
y-intercept:
What are the slope and y-intercept of 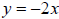 ?
?
slope:
y-intercept:
(b) Use this information from part (a) to draw neat graphs of the two functions
on the grid
below. Use a straight-edge to draw each line.
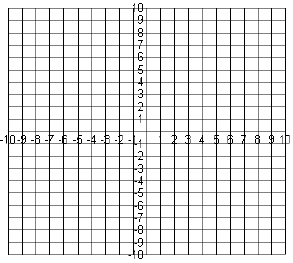
(c) From your graph, determine the coordinates of the
point of intersection of the two lines.
Substitute the values you found into each equation. If both equations are
satisfied, then
you have correctly used graphing to solve the given system of equations
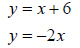
2. Follow the procedure outlined in problem #1 to solve the given system of
equations.
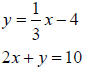
Answer:

3. Follow the procedure outlined in problem #1 to try to
solve each of the systems below.
Can you find a solution? If not, in each case, why not?
II. Solving systems of Linear Equations Algebraically
Systems of linear equations can be solved algebraically
using either the Substitution Method or
the Elimination Method .
The Substitution Method
To solve a system of equations using the substitution method,
• Solve one of the equations for one of the variables
• Substitute this expression into the other equation.
• Solve for the remaining variable
• Substitute the value you just found into one of the equations to get the other
variable
• Check the answer in both of the original equations
Example: Solve the system of equations 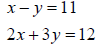 using
the substitution method.
using
the substitution method.
• Solve the first equation for one of
the variables. In
this case, solve for x in the first equation because it
is the easiest one to solve for |
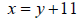
|
| • Substitute this expression into the
second equation. |
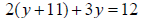 |
| • Solve for the remaining variable |
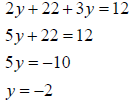 |
| |
• Substitute the value you just found
into one of the
equations to get the other variable. |
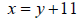 or or
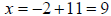
|
| • Check the answer in both of the
original equations. |
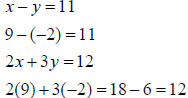 |
| |
Both equations check, so the answer is (9, -2)
4. Use the substitution method to solve each of the following systems of
equations. If it is
not possible to find a unique solution for the system , why not?
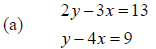
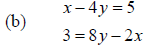
The Elimination Method
To solve a system of equations using the elimination method,
• Multiply one or both equations by constants that will create a new system in
which one of
the variables has coefficients that are the opposite of one another, that is,
the coefficients
are the same number in absolute value but have opposite signs
• Add the two new equations together. One variable should be eliminated.
• Solve for the remaining variable
• Substitute the value you just found into one of the equations to get the other
variable
• Check the answer in both of the original equations
Example: Solve the system 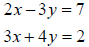 by the method of
elimination
by the method of
elimination
• Multiply one or both equations by
constants that will create a new system in
which one of the variables has
coefficients that are the opposite of one
another, that is, the coefficients are the
same number in absolute value but have
opposite signs |
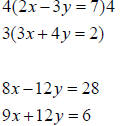 |
• Add the two new equations together.
One
variable should be eliminated. |
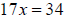
|
| • Solve for the remaining variable |
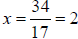 |
• Substitute the value you just found
into
one of the equations to get the other variable |
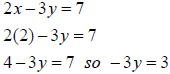 and and
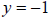 |
| |
• Check the answer in both of the
original
equations |
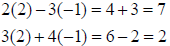 |
Both equations check, so the answer is (2, -1)
5. Use the elimination method to solve each of the following systems of
equations. If it is
not possible to find a unique solution for the system, why not?