17.3 Accept on faith that the following familiar functions
are continuous on their domains:
sin(x), cos(x), ex, 2x, loge(x) for x > 0, xp for x > 0 [p any real number].
Use these
facts and theorems in this section to prove that the following functions are
also continuous.
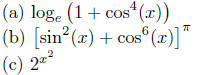
Solution : (a) Notice that cos4(x) = (b ◦ a)(x), where a(x) = cos(x) and b(x) = x4.
Since
a and b are continuous, so is cos4(x) by Theorem 17.5. Since 1 is also
continuous, Theorem
17.4 says c(x) = 1 + cos4(x) is continuous. Finally, loge(1 + cos4(x))
= (d ◦ c)(x) where
d(x) = log e(x). Since d and c are continuous, Theorem 17.5 tells us that loge(1 + cos4(x))
is continuous.
(b) Well, a(x) = x2 and b(x) = sin(x) are continuous, so (a
◦ b)(x) = sin2(x) is
continuous
by Theorem 17.5. Similarly, c(x) = x6 and d(x) = cos(x) are continuous, so (c
◦ d)(x) =
cos6(x) is continuous by Theorem 17.5. Then Theorem 17.4 tells us that e(x) =
sin2(x) +
cos6(x) is continuous. Finally,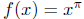 is continuous, so Theorem 17.5 says (f
◦ e)(x) =
is continuous, so Theorem 17.5 says (f
◦ e)(x) =
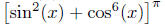 is continuous.
is continuous.
(c) Well, a(x) = x2 and b(x) = 2x are continuous, so by Theorem 17.5, (b
◦ a)(x) =
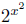 is
is
continuous.
17.5 (a) Prove that if m ∈ N, then the function
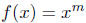 is continuous on R.
is continuous on R.
(b) Prove that every polynomial function
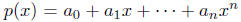
is continuous on R.
Proof: [of (a)] By induction on m. For m = 1, we need to show that p(x) = x is
continuous
at any a ∈ R. For any ε > 0, taking δ = ε we get
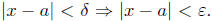 Hence,
p is
Hence,
p is
continuous on R.
Now assume that
 is continuous and show that
is continuous and show that
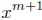 is continuous. But
is continuous. But
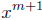 =
=
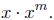 . We showed above that x is continuous, and the induction hypothesis is that
. We showed above that x is continuous, and the induction hypothesis is that
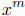 is
is
continuous. By Theorem 17.4(ii),
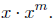 is continuous.
is continuous.
By induction, then,
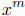 is continuous for every m
∈ N.
is continuous for every m
∈ N.
(b) By (a),
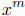 is continuous for any m
∈ N. Hence, by Theorem 17.3, a
is continuous for any m
∈ N. Hence, by Theorem 17.3, a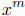 is
continuous
is
continuous
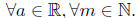 By 17.4(i) and induction, any polynomial is continuous .
By 17.4(i) and induction, any polynomial is continuous .
Formally, we prove by induction that
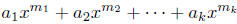 is continuous for
is continuous for
any k. The case k = 1 was done in the first paragraph. Now assume that
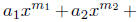
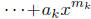 is continuous and show that
is continuous and show that
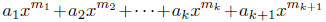 is continuous.
is continuous.
But
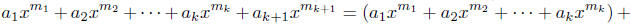
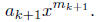 By (a),
By (a),
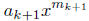 is continuous, by the induction hypothesis,
is continuous, by the induction hypothesis,
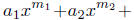
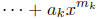 is continuous. Hence, by Theorem 17.4(i),
is continuous. Hence, by Theorem 17.4(i),
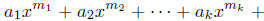
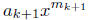 is continuous.
is continuous.
Therefore, any polynomial function
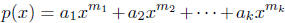 is continuous
is continuous
on R.
17.9 (a) Prove that the following function is continuous at
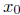 by verifying the
by verifying the
 property of Theorem 17.2.
property of Theorem 17.2.
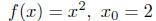
Solution : Scratch work: We need
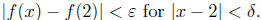 So we need
So we need
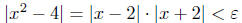
Now if
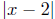 is small, say
is small, say
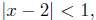 then
-1 < x < 3, so 1 < x + 2 < 5.
Hence,
then
-1 < x < 3, so 1 < x + 2 < 5.
Hence,
if
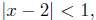 then
then
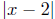 < 5 and so
< 5 and so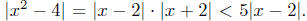 . So we want
. So we want
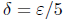 or 1, whichever is smaller.
or 1, whichever is smaller.
Proof: Given ε > 0 let δ =
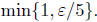 Then
Then
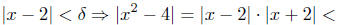
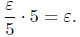 Hence, f(x) = x2 is continuous at
Hence, f(x) = x2 is continuous at
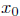 = 2.
= 2.
17.12 (a) Let f be a continuous real -valued function with domain (a, b). Show
that if f(r) = 0 for each rational number in (a, b), then f(x) = 0 for all
x ∈ (a, b).
(b) Let f and g be continuous real - valued functions on (a, b) such that
f(r) = g(r) for each rational number r in (a, b). Prove that f(x) = g(x)
for all x ∈ (a, b).
Solution : (a) Since f is continuous, for any convergent sequence (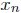 ) in (a, b),
converging
) in (a, b),
converging
to 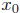 in (a, b), we have lim f(
in (a, b), we have lim f(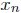 ) = f(
) = f(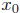 ). Now let
). Now let
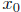 be any number in (a, b).
There is a
be any number in (a, b).
There is a
sequence of rational numbers (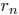 ) in (a, b) converging to
) in (a, b) converging to
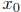 . [By the denseness
of Q, see
. [By the denseness
of Q, see
§11 Example 3.] But then lim f(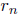 ) = lim 0 = 0 so f(
) = lim 0 = 0 so f(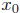 ) = 0. That is, f(x) = 0
for any
) = 0. That is, f(x) = 0
for any
x ∈ (a, b).
(b) Consider h(x) = f(x) - g(x) on (a, b). Then h(r) = 0 for all rational numbers
r ∈ (a, b).
By part (a), h(x) = 0 for all x ∈ (a, b), so f(x) = g(x) for all x ∈ (a, b).
18.5 (a) Let f and g be continuous function on [a, b] such that f(a)
≥ g(a) and
f(b) ≤ g(b). Prove that f(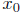 ) = g(
) = g(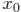 ) for at least one
) for at least one
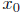 in [a, b].
in [a, b].
(b) Show that Example 1 can be viewed as a special case of part (a).
Solution: (a) Since f and g are continuous on [a, b], h(x) = f(x)
-g(x) is also
continuous
on [a, b]. Further, since f(a) ≥ g(a) we have h(a) ≥ 0, and since f(b) ≤ g(b), we have
h(b) ≤ 0. So by Theorem 18.2, there is at least one point
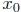 ∈ [a, b] such that
h(
∈ [a, b] such that
h(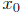 ) = 0.
) = 0.
At that point, f(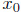 ) = g(
) = g(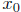 ).
).
(b) Example 1 says that any continuous function f : [0, 1]
→ [0,1] has a xed
point. We
obtain this statement from (a) by letting g(x) = x.
18.7 Prove that 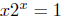 for some x in (0, 1).
for some x in (0, 1).
Proof: Let f(x) = 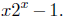 Notice that f is continuous on R, since x, 2x and 1
are (using
Notice that f is continuous on R, since x, 2x and 1
are (using
Theorem 17.4(i, ii)). Notice further that f(0) = -1 and f(1) = 1. Since -1 < 0
< 1,
Theorem 18.2 says there is at least one x ∈ (0, 1) where f(x) = 0. For that x,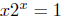 .
.
18.10 Suppose that f is continuous on [0, 2] and that f(0) = f(2). Prove that
there exist x, y in [0, 2] such that 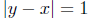 and f(x) = f(y).
and f(x) = f(y).
Proof: Consider g(x) = f(x + 1) - f(x). Since x + 1 is continuous on [0, 2],
Theorem
17.5 says f(x + 1) is continuous on [0, 1]. Then Theorem 17.4(1) says g(x) is
continuous
on [0, 1].
Notice that g(0)+g(1) = f(1) - f(0)+f(2) - f(1) = f(2) - f(0) = 0, so g(1) =
- g(0).
Either g(1) = g(0) = 0, in which case x = 0 and y = 1 satisfy the statement we
are to
prove, or g(1) and g(0) are on opposite sides of 0. In that case, Theorem 18.2
implies that
there is at least on point 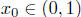 such that
such that
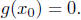 At that point, f(
At that point, f(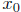 )
= f(
)
= f(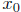 +1),
+1),
so letting x = 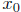 and y =
and y =
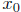 + 1 we get the conclusion.
+ 1 we get the conclusion.



