Next Quarter
The class next quarter will be on 10 Monday nights same
time
(5:00 PM -8:15 PM) same place (Munroe School)
starting Monday, March 30 and ending Monday, June 8. Class
will not be held on Memorial Day, Monday, May 25 or Monday
April 6.
Today
inequalities in two
variables
‘conjugates’ and rational /real coefficients
Yao and what is ‘ solving an equation ’
Harel and ‘guess, check, and generalize’
minimax problems
evaluations
questions
exam discussion
Homework analysis
1. Solve the following system inequalities graphically
using your
graphing calculator and turn in a sketch of the graph with the
region satisfying the inequalities shaded.
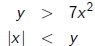
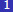What sort of object is
the solution?
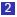How can it be described? What are the
intersection
points?
calculator screen size; use z-box
Difference of Squares - conjugates
CME 665: 12, 13
Extend to i. Return to 664: 10, 11
Imaginary roots and quadratics
Ask someone to explain the correct solution to CME 664
numbers 10-11.
Yao
Consider the following argument.
Let H be your height, Y be Yao’s height and A be the average
of the two heights, (H + Y )/2. Then H + Y = 2A so that:
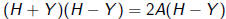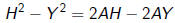or
or
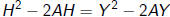
or, adding A 2 to both sides of the equation
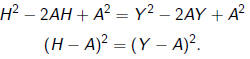
Thus, H − A = Y − A or H = Y . You are indeed as tall as
Yao! If you do not think you can ever be as tall as Yao, find
the flaw in this argument.
What is a written solution of an
equation/inequality
It is a series of deductions about any number(s) that
might
satisfy the
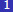equation
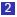inequality
system of equations
system of inequalities
Moral
If the solution is correct, each line implies the next.
In the case of Yao, the conclusion that if two numbers have the
same square they are equal was incorrect.
In other cases, (next quarter), the implication may be correct
but The two statements may not be equivalent.
So the result is a candidate solution.
Any solution will satisfy the last line.
Not every number that satisfies the last line has to be a
solution.
Harel
See handout. Taken from Harel’s DNR as a conceptual
framework.
Maximizing area
CME 710 problem 8
Look at problem 10 on that page.
Make up a similar but more complicated problem where there
are different constraints on the perimeter (including internal
walls) but the area is maximized.
Course Summary for Exam
Each topic may be addressed either in a concrete situation
or
as pure mathematics problem.
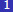Solution of systems of linear equations .
Graphs of linear equations
modeling
What does it mean to have no or infinitely many solutions
Solution of systems of linear inequalities ( in one unknown )
Solution of systems of linear inequalities (in two
unknowns)
absolute value including solutions of inequalities and
equations in one or two variables
Finding exact solutions; finding approximate solutions
graphically
Normal forms for linear and quadratic equations
Properties of quadratic functions and their graphs
Solutions of quadratic equations (factoring, completing
the square, quadratic formula )
representing functions by formulas, graph, table
Transformation of quadratics and the effect on the graph
understanding the logic of equation/inequality solutions
the zero product property and other properties of the real
numbers
minimizing or maximizing quadratic functions
the function notion
Find at least one problem from the homework or from the CME
text that addresses each of these topics and solve it. Some of
the topics are broad enough so that you should look at several
different problems. Look for connections between the various
topics. Try to see how the same concrete situation can be
solved using different topics.
