Math 265 is a first course in Linear Algebra (Math 365 is
a second course). Over
75% of all mathematical problems encountered in scientific or industrial
applications
involve solving a system of linear equations . Linear systems arise in
applications
to areas such as business, demography, ecology, electronics, economics,
engineering,
genetics, mathematics, physics, and sociology. Linear algebra involves much more
than solving systems of linear equations, it also involves abstract and
geometric
thinking. You will have to use analogies, and learn to think geometrically in
more than
3 dimensions. Linear algebra is commonly the first course that a student
encounters
that requires abstract thought. For this reason, students all over the world
struggle
when they first meet linear algebra. If you can not devote at least 8 productive
hours
of work per week to this course, then I recommend you take this course later
when
you can devote the necessary time and effort.
Calculators and computers can be very useful as an aid to computation, for
checking
hand computations, and as a laboratory for quickly exploring new ideas. I
encourage
the intelligent use of calculators and computers. My discussions about
calculator
usage will be confined to the TI83 Plus. You will likely need to improve the
accuracy
and speed of your arithmetic : calculators are not allowed on tests and the final
exam.
In particular, there exist links for practising arithmetic
and testing algebraic skills.
We shall cover chapters 1, 2, 3 (chapters 5, 6, 7 are covered in Math 365). I
should
stress though that the lecture notes, not the textbook, form the body of
examinable
material. I strongly encourage you to read the relevant parts of the textbook
before
attending lectures, review your lecture notes after each lecture, and do all the
assigned
problems! The way to become a good violin player is to practice. To become good
at
this course (and hence pass) you must practice. You will learn much more doing
the
exercises yourself than watching an expert solve them for you!
If you are unable to attend a lecture, you should get a copy of the notes from a
classmate who takes good notes. Consider forming your own study groups : you can
learn a lot by explaining solutions to a friend , and by hearing solutions.
After each test I will post adjacent to my office a list of scores and
approximate
grades, so you can determine your relative position in the class. You should
double-
check the time of the final exam by using Safari. The exam will be in our
assigned
classroom.
Students requiring special accommodation, because of a physical or mental
disabil-
ity, should see me in the first week of the course. Also, if you are quite sick
or suffer
a notable hardship, then please let me know promptly. Claims of lengthy hardship
that are disclosed the day before the final exam receive less sympathy. Although
the
Registrar will notify you of your final grades, you can find out your
(unofficial) grades
earlier by using Safari.
I plan to make each Tuesday a problem-solving class. Please bring your
textbook
on these days. A brief description of the course content, and the approximate
number
of lectures spent on each topic is: solving systems of linear equations (4),
matrix
algebra and elementary matrices (4), determinants with applications to
areas/volumes
and computing inverses (5), vector spaces, subspaces, and dimension (7), the
matrix
of a linear transformation and change of basis (3). The course outcomes are: (i)
that
students learn to think abstractly, laterally, logically and critically , and
(ii) that
(passing) students have a reasonable mastery of the concepts underlying the
above
topics.
Math 265 Homework Problems
Below is a list of homework problems from the textbook, S. J. Leon, Linear
algebra
with applications, 7th ed., 2006. You should solve all homework problems before
Tuesday, and importantly you should write out your solutions neatly using
correct
notation, correct spelling, and grammatically correct English sentences. I shall
deduct
points on exams for poor setting out, especially for omitting brackets and equal
signs.
On problem-solving days you should bring your textbook, your worked solutions,
and
your questions. The chapter tests, abbreviated CT below, are helpful to test
your
knowledge before an exam.
§1.1, p.11 1cd, 2cd, 3bd, 5c, 6e, 10
§1.2, p.25 1, 2, 3, 5ef i, 10, 13, 17, 20*
§1.3, p.57 1abefg¤h¤, 2a–f, 4, 8, 15, 20, 22, 23
§1.4, p.69 1, 2, 3, 4b, 6, 9ab(i), 10, 11
§1.5, p.79 1abc, 11
CT1, p.87 1–9, 10*
§2.1, p.96 1, 3bcdg, 4abc, 11
§2.2, p.103 1, 2a, 3ac, 4, 5, 6, 7, 9, 12, Q1 below
§2.3, p.109 1, Q2 below
CT2A, p.113 1, 2, 3, 5–10
§3.1, p.121 4, 8, 9, 11, 15, 16
§3.2, p.131 1bce, 2abc, 4ab, 8, 9a, 10ae, 11, 12
§3.3, p.144 1, 2, 4, 5, 11
§3.4, p.150 1, 2, 3, 4, 5, 10, 16
§3.5, p.161 1, 2, 3, 5, Q3
CT3A, p.172 1–8
Q1 Compute the determinant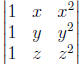
by using row
operations , and taking out
factors of y − x and z − x. Hence determine when the determinant is nonzero.
Q2 Compute the inverse of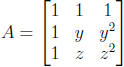 
. [Hint: det(A) =
(y − 1)(z − 1)(z − y).]
Q3 Let
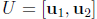be the ( ordered ) basis for R2 obtained by rotating the standard
basis
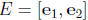by θ radians counterclockwise about the origin.
(i) Show that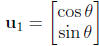 
and
.
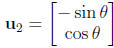(ii) Find the change of coordinate matrix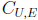 
from the basis E to the basis U.
