Linear Inequalities
The Properties of Linear Inequality are almost exactly like the ones for
linear equalities, except for
one very important difference :
When both sides of an inequality are multiplied or divided
by a negative number, the
direction of the inequality symbol is reversed .
The Properties of Linear Inequality are true for >, <, ≤
and ≥.
> means greater than
≥ means greater than or equal to
< means less than
≤ means less than or equal to
Linear equations have one single solution. Linear
inequalities have infinitely many solutions. We
call this a solution set.
Example 1:
Find the solution set for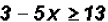 
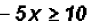
Now we have to divide both sides by a negative number!
Note that the inequality sign
changes direction when we divide or multiply by a negative number!
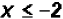
The solution set in Interval Notation is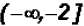 
Example 2:
Find the solution set for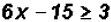
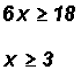
The solution set in Interval Notation is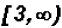 
Compound Inequalities
Compound inequalities contain two inequality signs, for example,
.
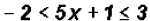In this case, we isolate x in the middle, applying
the Properties of Linear Inequality to the right and
left side of the inequality, as well as to the middle.
The inequality signs can be any combination of >, <, ≤ or
≥.
Example 1:
Find the solution set for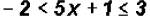 
.
Subtracting 1 from the left and right side of the inequality and from the
middle, we get
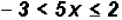
Dividing 5 into the left and right side of the inequality, and into the
middle, we get
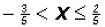
The solution set in Interval Notation is
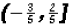
Example 2:
Find the solution set for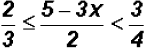 
With this type of inequality, it is best to clear fractions immediately. Simply
multiply each
part by the common denominator taking all given denominators into account.
The LCD is 12 !!!
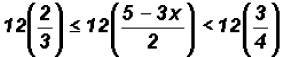
Reducing fractions, we get
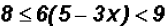
and using the Distributive Property
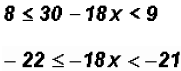
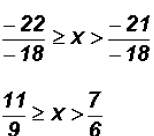
It is standard procedure in compound inequality to have all inequality signs
point to the
left, therefore, we rearrange our terms without changing the solution set
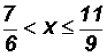
The solution set in Interval Notation is
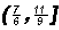
Absolute Value Inequalities
Solution Strategy
Rewrite absolute value inequalities without absolute value
bars. The number c must be positive by
definition of absolute value!!!
These rules are also valid if the inequality sign is
strictly < or >.
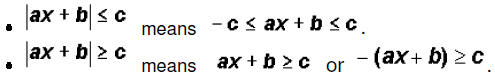
In the second case, you have to solve both
inequalities!!! The word "or" is a part of the
formula and must be there. It does not mean that you can use either one of the
inequalities
when you solve for the unknown.
Example 1:
Find the solution set for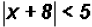 
By definition above, the "less than" case is rewritten as a compound inequality
as follows
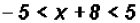
Isolating the variable in the middle , we get
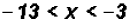
The solution set in Interval Notation is
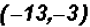
Example 2:
Find the solution set for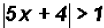 
By definition above, the "greater than" case is rewritten as two inequalities as
follows
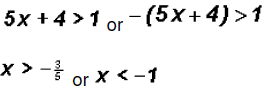
The solution set in Interval Notation is
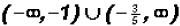
Example 3:
Find the solution set for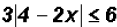 
Before we apply the definition, we MUST first isolate the absolute value as
follows
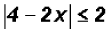
Next, we will rewrite the "less than or equal to" case as a compound inequality
according
to the above definition
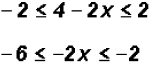
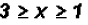Note that the inequality signs changed
direction because we divided by
a negative number !
Changing the solution set to standard form, we get
.
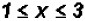The solution set in Interval Notation is [1, 3]
