Section 2.2: Solving Systems of Linear Equations I
As you may recall from College Algebra , you can solve a
system of linear equations in
two variables easily by applying the substitution or addition method. Since
these
methods become tedious when solving a large system of equations, a suitable
technique
for solving such systems of linear equations of any size is the Gauss-Jordan
elimination
method. This method involves a sequence of operations on a system of linear
equations
to obtain at each stage an equivalent system .
Given the following system of equations:
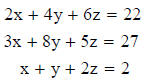
the coefficient matrix is: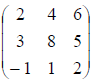
the augmented matrix is: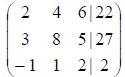
We will use the
augmented matrix.
When using the Gauss-Jordon elimination method using very
strict rules will look like:
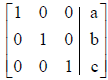Where a, b and c (a, b and c are numbers)
are the values for x , y and z
respectively.
Row Operations
1. Interchange any two rows.
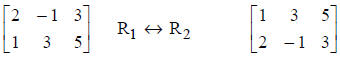
2. Replace any row by a nonzero constant multiple of
itself.
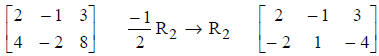
3. Replace any row by the sum of that row and a constant
multiple of any other row.
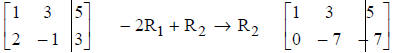
Pivoting a Matrix About an Element
The sequence of row operations that transforms the
augmented matrix into the equivalent
matrix in which the 1st column is transformed into the unit column is called
pivoting the
matrix about the element that transformed into 1 (leading 1).
Example: Given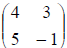 
To change the column 
into the unit column 
we perform certain row
operations and we call
this pivoting the matrix about the element 4.
Example 1: Pivot the following matrix about the
circled element.
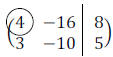
The Gauss-Jordan Elimination Method
1. Write the augmented matrix corresponding to the linear
system.
2. Interchange rows (operation 1), if necessary, to obtain
an augmented matrix in which the
first entry in the first row is nonzero. Then pivot the matrix about this entry.
3. Interchange the second row with any row below it, if
necessary, to obtain an augmented
matrix in which the second entry in the second row is nonzero. Pivot the matrix
about this
entry.
4. Continue until the final matrix is in row- reduced form .
Example 2: Solve the system of linear equations
using the Gauss-Jordan elimination method.
2x + 4y = 1
3x + 4y = −1
Example 3: Solve the system of linear equations
using the Gauss-Jordan elimination method.
5x − 2y = 16
−2x − y= 1
Row Reduced Form
An m x n augmented matrix is in row-reduced form if it
satisfies the following conditions:
1. Each row consisting entirely of zeros lies below any
other row having nonzero entries.
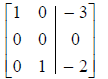the correct row-reduced form
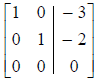
2. The first nonzero entry in each row is 1 (called a
leading 1).
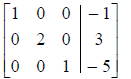the correct row-reduced form
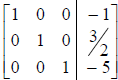
3. In any two successive (nonzero) rows, the leading 1 in
the lower row lies to the right of the
leading 1 in the upper row.
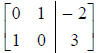the correct row-reduced form
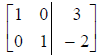
4. If a column contains a leading 1, then the other
entries in that column are zeros.
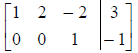the correct row-reduced form
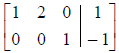
Unit Column: A column in a coefficient matrix is in unit
form if one of the entries in the
column is a 1 and the other entries are zeros.
Example 4: Determine which of the following
matrices are in row-reduced form. If a matrix
is not in row-reduced form, state which condition is violated.
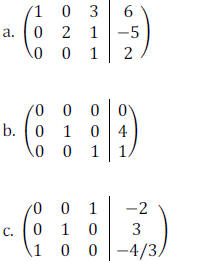
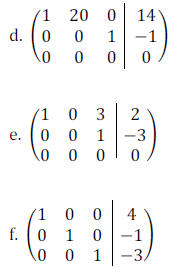
Example 5: Solve the system of linear equations using the Gauss-Jordan
elimination method.
x+ 3y + 3z = 4
2x + 4y − 3z = −1
3x − 5y − 3y = 0
Example 6: Solve the system of linear equations
using the Gauss-Jordan elimination method.
2y − 3x = −4
x − 3y + 2y = 0
5y + 4z = 13
Example 7: You invested a total of $40,000 in two
municipal bonds that have a yield of 5%
and 7% interest per year, respectively. The interest you earned from the bonds
was $2,360.
How much did you invest in each bond? Use the Gauss-Jordan elimination method to
solve.
Section 2.3
Solving Systems of Linear Equations II
In the previous section we studied systems with unique
solutions. In this section we will
study systems of linear equations that have infinitely many solutions and those
that have
no solution. We also will study systems in which the number of variables is not
equal to
the number of equations in the system.
A System of Equations with an Infinite Number of
Solutions
Example 1: The following augmented matrix in
row-reduced form is equivalent to the
augmented matrix of a certain system of linear equations. Use this result to
solve the
system of equations.
A System of Equations That Has No Solution
Example: Given the following system
In using the Gauss-Jordan elimination method the following
equivalent matrix was
obtained (note this matrix is not in row-reduced form, let’s see why):
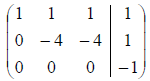
Look at the last row. It reads: 0x + 0y + 0z = -1, in
other words, 0 = -1!!! This is never
true. So the system is inconsistent and has no solution.
Systems with No Solution
If there is a row in the augmented matrix containing all
zeros to the left of the vertical
line and a nonzero entry to the right of the line, then the system of equations
has no
solution.
Theorem
I. If the number of equations is greater than or equal to
the number of variables in a
linear system, then one of the following is true:
a. The system has no solution.
b. The system has exactly one solution.
c. The system has infinitely many solutions.
II. If there are fewer equations than variables in a
linear system, then the system either
has no solution or it has infinitely many solutions.
Example 2: Solve the system of linear equations
using the Gauss-Jordan elimination
method.
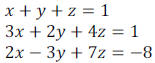
Example 3: Solve the system of linear equations
using the Gauss-Jordan elimination
method.
x − 2y = 4
2x + 4y = −3
3x + y = 2
Example 4: Solve the system of linear equations
using the Gauss-Jordan elimination
method.
x − 3y = −4
4x − 12y = −16
−2x + 6y = 8
Example 5: Solve the system of linear equations
using the Gauss-Jordan elimination
method.
−3x + 2y+ 5z = −1
6x − 4y− 10z = 10
