Definition: A l i n e a r equation can be written in the form Ax + By = C.
Note: These equations are called linear because their graphs are always lines.
Question: Which linear equations are functions?
Answer: All lines except vertical lines are functions.
Definition: A l i n e a r function can be written in the form f(x) = mx + b.
This is also referred to as the slope-intercept form of
a line, where m is the slope and b is the y -intercept.
Note: The slope is the ratio (or comparison) of the change in y divided by the
change in x. A good way to remember slope is to
use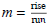 
.
To graph a linear function we need to recall a fact from geometry. We will use
the fact that any two points define a line. Thus to
graph a linear function we need only find two solution points to the linear
equation. There are many ways to accomplish this.
Method 1: Use any Two Points
Example1: f(x) = 2 x - 3
Solution : We need to find two solution points.
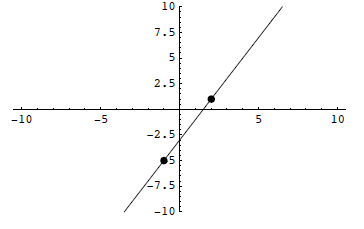
Example 2: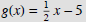 
Solution:
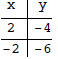
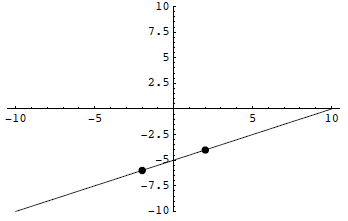
Method 2: Use the Intercepts
The intercepts are the points where the graph crosses each axis. There are
x-intercepts and y-intercepts. We find the x-intercepts by letting y = 0 and the
y-intercepts by letting x = 0.
Example 1: h(x) = -3 x - 6
Solution: The y-intercept is (0, -6).
To get the x-intercept let y = 0.
0 = -3 x - 6
6 = -3 x
x = -2
The x-intercept is(-2, 0).
Example 2: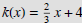
Solution: The y-intercept is (0, 4).
To get the x-intercept.
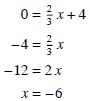
So the x-intercept is (-6, 0).
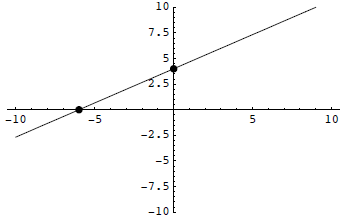
Method 3: Use the Slope and y -intercept
We can use the slope and intercept of the line to sketch it. Start by plotting
the y -intercept and then use the slope
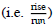as a map to find a second point.
Example 1: s(x) =-4 x + 1
Solution: Start with the y-intercept (0, 1), them from move down 4 and
right 1. This gives the point (1,-3).
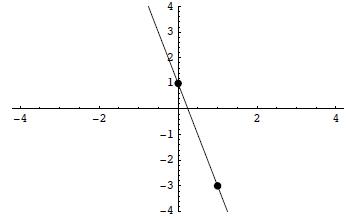
Example 2:
Solution:
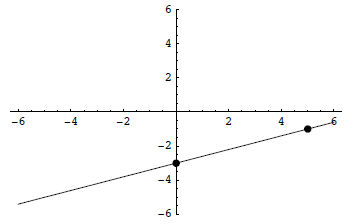
To write the linear function that passes through two points , we'll use the
slope-intercept form f(x) = m x + b. This means we must first find the slope of
the line and then find the y-intercept.
Example 1: Find the equation of the linear function passing through the
two points (2,1) and (0,3). Then write the equation
using function notation.
Solution: First we need to find the slope.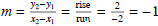
So this tells us that the function is of the form y = -x + b.
To get b, we'll note that the point (0, 3) is the y-intercept and so b = 3.
So our linear function is f(x) = -x + 3
Example 2: Find the equation of the linear function passing through the
two points (3,6) and (-3,2). Then write the equation
using function notation.
Solution:
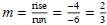
So this tells us that the function is of the form
.
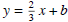To find b, take one of the points and substitute and then solve .
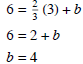
So the linear function is
Note: There is an alternate way to find the equation of a line. We can
use point-slope form of a line. y - y1 = m(x - x1)
Example 3: Find the equation of the linear function passing through the
two points (5, -3) and (-10, 3). Then write the
equation using function notation.
Solution: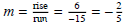 
.
So the equation is given by 
.
Now to get this into function form we need to solve for y and simplify .
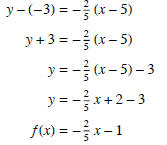
Parallel and Perpendicular Lines
Theorem:
Two lines are parallel if they have equal slopes.
Two lines are perpendicular if they have opposite reciprocal slopes .
i.e. If the first line has slope 
, then the
second has slope - 
.
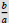Example 1: Find the equation of the line passing through the point (1,5)
and parallel to the line 4 x + 2 y = 1.
Solution: First we need to find the slope. Since the new is parallel to 4
x + 2 y = 1, we need to find the slope of this line. We can do this by solving
for y and getting slope-intercept form.
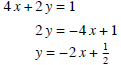
So m = -2.
So our new line is of the form y = -2 x + b.
5 = -2(1) + b
b = 7
So the new linear function is f(x) = -2 x + 7.
Example 2: Find the equation of the line passing through the point (2,1)
and perpendicular to the line 2 x + 3 y = 15.
Solution: We need to find the slope of 2 x + 3 y = 15.
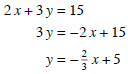
So 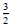m =
, since the new
line is perpendicular. So it is of the form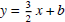
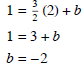
So the new function is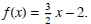
.
