Factoring Polynomials

Some trinomials that can be factored do not look like the special trinomials from the
previous sections . Factor trinomials, written ax² + bx + c, by doing the following rules:

1. Factor out the GCF of all three terms. Use the resulting trinomial for the rest of
the steps. If a is negative, also factor out –1 along with the GCF.

2. Check that the square root of b² – 4ac is a whole number. If b² – 4ac is negative,
then we cannot factor the trinomial. If the square root of b² – 4ac is not a whole
number, then the factored form of ax² + bx + c will have fractions or square root
signs in it . We will not be factoring these in this section.

3. Look at the sign of the constant term.

a. If the second sign (the one before the constant term) is a + sign, then both signs
in the factored form are whatever the first sign is.
ax² + bx + c = ( __ + __ )( __ + __ )
or
ax² – bx + c = ( __ – __ )( __ – __ )

b. If the second sign is a – sign, then the signs in the factored form are different .
ax² + bx – c = ( __ + __ )( __ – __ )
or
ax² + bx – c = ( __ + __ )( __ – __ )

4. Find two numbers that multiply together to give ac but add up to give b. Keep the
signs of a, b, and c with the numbers.

5. Rewrite in preliminary factored form:
a. Write the GCF on the outside of the factored form.
b. In both sets of the parentheses, write ax
c. Write the appropriate signs from step 3.
d. Write the two numbers found in step 4, one in each set of parentheses.

6. Factor out any GCFs from the sets of parentheses and throw them away.

7. Rewrite. This is the final factored form.

Examples:
1. Factor 3x² + 5x + 4.
Step 1: Find GCF(3x², 5x, 4). The GCF is 1 since none of the coefficients have a
factor in common .
Step 2: Find b² – 4ac. In this trinomial, a = 3, b = 5, and c = 4, so
b² – 4ac = (5)² – (4)(3)(4) = 25 – 48 = -23. Since -23 is negative, we cannot factor
this polynomial.

2. Factor x² + 5x + 6.
Step 1: Find GCF(x², 5x, 6). The GCF of this trinomial is 1 since the only factor of
1 is 1.
Step 2: Find b² – 4ac. Here, a = 1, b = 5, and c = 6, so b² – 4ac = (5)² – (4)(1)(6) =
25 – 24 = 1. Since 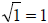, a whole number, then we can factor this trinomial and
have integer coefficients.
Step 3: Sign of the constant term. The constant term of this trinomial is +6, so both
the signs inside the factored form (a.k.a. the answer) will be the same. Since the
sign on the 5x is positive also , the factored form will look like ( __ + __ )( __ + __ ).
Step 4: Find 2 numbers. We need two numbers that multiply together to give (1)(6)
= 6 and add up together to give 5. Factors of 6 are 1 & 6 or 2 & 3. Since 2 + 3 = 5,
these are the numbers we will use.
Step 5: Preliminary answer. The preliminary factored form is 1(1x + 2)(1x + 3).
Step 6: Internal GCFs. There are no GCFs other than 1 inside each set of
parentheses.
Step 7: Rewrite. The factored form is (x + 2)(x + 3)

3. Factor the polynomial x ² – 5x – 24.
Step 1: GCF(x², -5x, -24) = 1.
Step 2: b² – 4ac = (-5)² – 4(1)(-24) = 25 + 96 = 121. 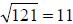, so we can factor
this polynomial.
Step 3: The sign of the constant term is negative, so the signs inside the sets of
parentheses will be different, ( __ + __ )( __ – __ )
Step 4: We want 2 numbers that multiply together to give (1)(-24) = -24 and add up
to -5. Factors of -24 and their sums are

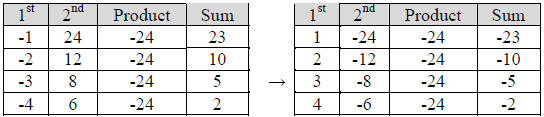
The numbers 3 and -8 multiply together to give -24 and add up to -5.
Step 5: The preliminary answer is 1(1x + 3)(1x – 8).
Step 6: Neither set of parentheses have a GCF other than 1.
Step 7: The answer is (x + 3)(x – 8).

4. Factor x² + 10x + 18.
Step 1: GCF(x², 10x, 18) = 1.
Step 2: b² – 4ac = (10)² – (4)(1)(18) = 100 – 72 = 28. Since 28 is not a perfect
square (the square root of 28 is not a whole number), we cannot factor this trinomial
and have only integer coefficients in our answer . This trinomial is in its final
factored form.

5. Factor 2x² + 18x – 72.
Step 1: GCF(2x², 18x, 72) = 2. We must factor 2 out of our trinomial:
2x² + 18x – 72 = 2(x² + 9x – 36). Use the trinomial inside the parentheses for the
rest of the problem.
Step 2: b² – 4ac = (9)² – 4(1)(-36) = 81 + 144 = 225. Since 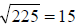, we can
continue with factoring.
Step 3: The constant term is negative, so the signs inside the sets of parentheses in
our answer will be opposite; that is, ( __ + __ )( __ – __ ).
Step 4: Find 2 numbers that add up to +9, but multiply to get (1)(-36) = -36:

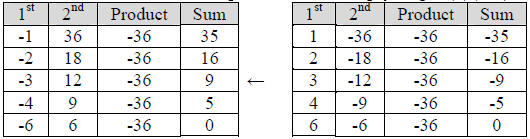
The numbers -3 and 12 multiply together to get -36 and add together to get 9.
Step 5: The preliminary answer is 2(1x + 12)(1x – 3).
Step 6: Neither set of parentheses have a GCF other than 1.
Step 7: The factored form is 2(x + 12)(x – 3).

6. Factor the trinomial 6x² – 27x + 12.
Step 1: GCF(6x², -27x, 12) = 3, so factor 3 out of the trinomial: 6x² – 27x + 12 =
3(2x² – 9x + 4). The trinomial 2x² – 9x + 4 will be used for the rest of the steps.
Step 2: b² – 4ac = (-9)² – 4(2)(4) = 81 – 32 = 49. 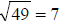, so we can factor.
Step 3: The constant term (12) is positive, so both sets of parentheses will have the
same sign. Since the sign of the middle term (-27x) is negative, the sets of
parentheses will look like ( __ – __ )( __ – __ ).
Step 4: Find two numbers that multiply together to give (2)(4) = 8 but add up to -9:

The numbers -1 and -8 are factors of 8 with a sum of –9.
Step 5: The preliminary answer is 3(2x – 1)(2x – 8).
Step 6: The second set of parentheses, the (2x – 8) part, has a GCF of 2, so divide
everything in this set of parentheses by 2 and discard the 2:
Step 7: The final factored form of 6x² – 27x + 12 is 3(2x – 1)(x – 4).

7. Factor –20x³ – 80x² – 75x.
Step 1: GCF(-20x³, -80x², -75x) = -5x. Since the coefficient of the term with the
highest order is negative, we want to pull the negative out along with the GCF.
Factor out the -5: -20x³ – 80x² – 75x = -5x(4x² + 16x + 15).
Step 2: b² – 4ac = (16)² – 4(4)(15) = 256 – 240 = 16. Since 16 is a perfect square,
we can factor the trinomial 4x² + 16x + 15.
Step 3: The constant and the middle terms are positive, so 4x² + 16x + 15 will factor
into something that looks like ( __ + __ )( __ + __ ).
Step 4: Find two numbers that multiply to give (4)(15) = 60 but add up to 16:

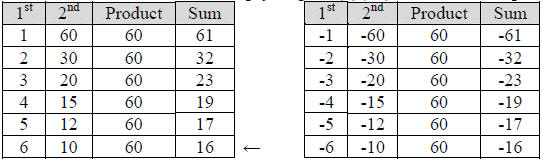
The numbers 6 and 10 are factors 60 and have a sum of 16.
Step 5: The preliminary answer is -5x(4x + 10)(4x + 6).
Step 6: Both sets of parentheses have GCFs greater than one. GCF(4x, 10) = 2 and
GCF(4x, 6) = 2. Divide everything in the first set of parentheses by 2 and everything
in the second set of parentheses by 2, throwing away the GCFs afterward:

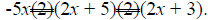
Step 7: Rewrite; the answer is -5x(2x + 5)(2x + 3).

Factor the following polynomials using any method . The answer should have only
integer coefficients.
1. x² + 7x + 6

2. x² + 2x + 1

3. 4x³ – 9x

4. 15x⁴ + 15x²

5. 2x² + 8x + 4

6. -12x² + 17x – 6

7. 7x² – 14x – 56

8. –4x² + 40x – 84

9. 10x² – 13x – 3

10. 30x³ – 3x² – 9x

11. x⁴ + 3x² – 4

12. -18x³ + 54x² – 8x + 24