Section 4.3 -Gauss Elimination for Systems of Linear Equations
What is a linear equation?
What does it mean to solve a system of linear
equations?
What are the possible cases when solving a system of
linear equations?
Example 1: Solve the following system of linear
equations:
4x-5y = -30
2x+y = -8
Example 2: Solve the following system of linear
equations:
2x-y = 1
6x-3y = 12
Example 3: Solve the following system of linear
equations:
3x-7y = 4
6x-14y = 8
Example 4: Solve the following system of linear
equations:
2x+5y+8z = 9
4x-6y+3z = 5
-3x+2y-4z = 8
Note: We will first learn how to set-up the system in
these word problems. We will later return to
learn how to systematically solve these problems.
Example 5: Jennifer has made it through her ten
year class reunion. She is wanting to remember
how many former classmates, spouses, and former teachers attended the reunion.
She has
lost her records but recalls that the ticket sales totaled $4,775. She charged
$30 for each former
classmate, $25 for each spouse, and $20 for each former teacher. She recalls
that the number
of former classmates and spouses combined was 130 more than the number of former
teachers.
She also recalls that there were five times as many former classmates there as
spouses.
Help Jennifer remember the number of former classmates, spouses, and former
teachers that
attended the reunion.
Set-up the linear system:
Example 6: An investment club has $200,000
earmarked for investment in stocks. To arrive at
an acceptable overall level of risk, the stocks that management is considering
have been classified
into three categories: high-risk, medium-risk, and low-risk. Management
estimates that
high-risk stocks will have a rate of return of 15%/year; medium-risk stocks,
10%/year; and
low-risk stocks, 6%/year. The members have decided that the investment in
low-risk stocks
should be equal to the sum of the investments in the stocks of the other two
categories . Determine
how much the club should invest in each type of stock if the investment goal is
to have
a return of $20,000/year on the total investment. (Assume that all of the money
available for
investment is invested.)
Set-up the linear system:
Definitions:
• A matrix is an ordered rectangular array of numbers. A matrix
with m rows and n columns has size
m×n. The entry in the ith row and jth column is denoted by aij.
• Augmented Matrix: We can combine two matrices into one, visually
separating them by a vertical
line. This is useful when solving a system of equations.
Gauss-Jordan Elimination
This method allows us to strategically solve systems of linear equations. We
perform operations
on an augmented matrix that is formed by combining the coefficient matrix and
the
constant matrix as shown in the next example.
Example 7: Find the intial augmented matrix for the system of equations below:
a)
2x-4y = 10
y = 1-3x
b)
x1-2x2 = 10x3+5
8x2 = x1-3x3
4x1-3x3 = x2
The goal of the Gauss-Jordan Elimination Method is to get the augmented matrix
into Row
Reduced Echelon Form. A matrix is in Row Reduced Echelon Form when:
1. Each row of the coefficient matrix consisting entirely of zeros lies below
any other row having
nonzero entries.
2. The first nonzero entry in each row is 1 (called a leading 1)
3. In any two successive (nonzero) rows, the leading 1 in the lower row lies to
the right of the leading
1 in the upper row.
4. If a column contains a leading 1, then the other entries in that column are
zeros.
Note: We only consider the coefficient side (left side) of the augmented matrix
when determining
whether the matrix is in row-reduced echelon form.
Example 8: Are the following in Row Reduced Echelon form?
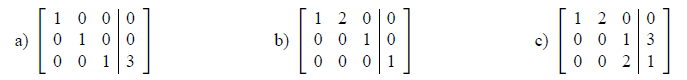
To put a matrix in Row Reduced Echelon Form, there are three valid
Row
Operations:
1. Interchange any two rows (Ri↔Rj)
2. Replace any row by a nonzero constant multiple of itself (cRi)
3. Replace any row by the sum of that row and a constant multiple of any other
row (Ri+cRj).
Steps for Gauss Jordan Elimination:
1. Begin by transforming the top left corner element, a11, into 1. This is your
first pivot element.
2. Next, transform the other elements in its column into zeros using the 3 row
operations.
3. Choose the next pivot element (diagonal down from the first pivot element)
4. Turn this 2nd pivot element into a 1, and transform the rest of its column
into zeros.
5. Continue until the coefficient matrix resembles the identity matrix(1’s along
the main-diagonal and
0’s everywhere else.)
Example 9: Solve the following system of equations using Gauss Jordan
Elimination:
3x+y = 1
-7x-2y = -1
Example 10: Solve the system that we set-up in Example 5.
Example 11: Solve the system that we set-up in Example 6.
Note: Our calculator will put an augmented matrix into row-reduced form for us.
This only
works when the # of rows is less than or equal to # of columns. Below are the
steps you must
follow
1. Enter the augmented matrix into your calculator.
2. Go to your home screen.
3. Press MATRIX , cursor right to MATH, and select B:rref.
4. Call the matrix you want to reduce and hit ENTER.
We will use the calculator for working the problems in the next section. You are
responsible
for knowing how to do the Gauss-Jordan Method by hand, but always remember that
you can
check your work with the calculator.
Section 4.4 - Systems of Linear Equations with Non -Unique Solutions
We are using the same process from Section 4.3 but now our solutions will not
always be unique.
Example 1: Solve the following system:
x+y+-2z = -3
2x-y+3z = 7
x-2y+5z = 0
Example 2: Solve the following system:
x+2y-3z = -2
3x-y-2z = 1
2x+3y-5z = -3
Example 3: Solve the following system:
x+y = 7
2x+3y = 8
4x-y = 3
Theorem: We have the following theorem concerning the number of equations and
the number of
variables in a system :
• If the number of equations is greater than or equal to the number of
variables, the system will have
either a unique solution, no solution, or infinitely many solutions.
• If the number of equations is fewer than than the number of variables, the
system will have either
no solution or infinitely many solutions.
Example 4: Solve the following system:
4x2-3x3-5x4 = 7
x1-2x2+3x4 = 8
Example 5: The rush hour traffic flow (the number of cars per hour) for a
network of four one-way
streets in a city is shown in the figure below:
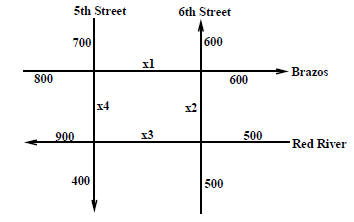
a) Determine the system of linear equations determined by the traffic flow at
each intersection.
b) Solve the above system.
c) What is the maximum number of cars that can travel from Brazos to Red River
on 5th street in an
hour?
d) If the traffic lights are adjusted so that 1,000 cars per hour drive on the
stretch in part (c), determine
the flow around the rest of the network.



