If A = B, then AC = BC.
(Multiplicative property of equality )
It is good practice to
identify (1) the lowest common denominator,
and (2) any numbers that would make the denominator equal to 0.
EX1. Solve: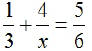
LCD:
x …≠
EX2. Solve: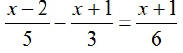
LCD:
x …≠
EX3. Solve: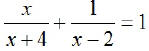 
LCD:
x …≠
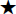A solution to an
equation is a value for the variable that makes the
original equation a true statement. Sometimes in the process of
solving an equation , a value for the variable is obtained that would
make one or more of the denominators equal to 0. Such a number
is not a solution of the original equation. It is called an extraneous
solution.
EX4. Solve: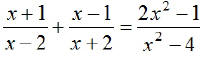
LCD:
x …≠
EX5. Solve: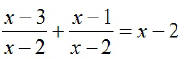 
LCD:
x …≠
EX6. D = RT (Solve for R)
EX7.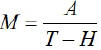 
(Solve for T)
EX8.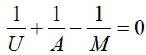 
(Solve for A)
EX9.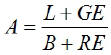 
(Solve for E)
EX10. EAT = EGGS -TSY (Solve for T)
DISTANCE-RATE-TIME Problems
D=RT
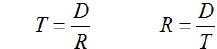
You may organize your data by completing the following
chart. You will
be given enough information to fill in two of the three columns (D-R-T).
Use the above formulas to fill in the other column. Although this type of
chart provides a useful way of organizing the data, it does not give the
required equation. You must read the problem carefully in order to put the
information in the chart into an appropriate equation for the problem.
EX11. Jermaine and Douglas both drove 100 miles from
Monticello to
Little Rock. Jermaine drove 10 mph faster than Douglas and
got to Little Rock 20 minutes earlier. How fast did each drive?
x = _________________________________
= _________________________________
Equation: _________________________________
Additional D-R-T Practice Problems:
1. Suppose that the time it takes a butterfly to fly 24
feet with a wind
that is blowing at 2 fps is 2 seconds less than the time that it would
take to fly 20 feet against a wind that is blowing at the same speed.
Find the speed at which the butterfly flies in still air.
2. A doctor drove 200 miles to attend a national
convention. Because
of the poor weather, her average speed on the return trip was 10 mph
less than her average speed going to the convention. If the return trip
took 1 hour longer, how fast did she drive in each direction?
3. The Little Rock Queen can make a 9 mile trip down the
Arkansas
River and return in a total of 1.6 hours. If the riverboat travels 12
mph in still water, find the speed of the current in the Arkansas River.
WORK Problems:
In the 1994 movie Little Big League, a young boy is given
the following
question for homework: “If Sam can paint a house in three hours and Joe
can paint the house in five hours, how many hours will it take for the two
of them to paint the house together?”
Answer: _________________________________
Note: The assumption for all problems of this type is that
a constant
rate of work is maintained throughout the course of the job or
task.
We will solve this type of problem using a geometric
representation of the
data. The rectangular stip that we will use represents both the total job and
the time required to complete it.
If Sam can paint the house by himself in 3 hours, how much
of the house
can he paint in 1 hour?
Answer: ___________________________________
If Joe can paint the house in 5 hours, how much of the
house can he paint
in 1 hour?
Answer: ___________________________________
How much of the house can Sam and Joe paint together in 1
hour?
Answer: ____________________________________
Draw a rectangular strip that represents one completed job
which in this
case would be one house completely painted. Since the two men are
working together, divide the strip into sections so that you can represent
how much of the job they do together in one hour.
Shade the number of sections of the strip that represents
the part of the job
that the two men can complete in one hour working together.
What does each section of the strip represent in terms of
time ?
Answer:________________________________
What does each section of the strip represent in terms of
the whole job?
Answer: ________________________________
Label the top of the strip with time units. Count the
number of shaded
sections that would be required to completely fill the strip.
Answer to original problem: _____________________________
Algebraic Solution:
Additional Practice Problems: Work
Example:Suppose that Eric can eat a small pizza in 5
minutes. His friend
Marcus can eat the same size pizza in 6 minutes. With each
eating at his usual rate, how long would it take them together
to eat a small pizza?
Estimate the time: ____________________________ minutes
We will solve this problem using a diagram and then we
will solve it using an
algebraic equation.
Practice Problem for Understanding: Suppose that it takes
a certain size
combine 8 hours to harvest the soybeans in a field. Another size
combine could harvest the soybeans in that field in 6 hours. If the
two combines were used together, how long would it take to harvest
the soybeans in the field?
Special Problem for Further Understanding: Refer to the
problem above
about harvesting soybeans. Suppose that the combine that takes 8
hours to harvest the soybeans has already been in the field 2 hours
before the other combine is available. How long would it take them
to finish harvesting the soybeans in that field together?
Really Special Problem for Understanding: Again refer to
the problem about
harvesting soybeans. Suppose that it takes 8 hours for one combine
to harvest the field of soybeans by itself. When it works with the
second combine, the work can be done in 6 hours. How long would it
take the second combine to harvest the field by itself?
Chapter 6: Section 6 Dividing Polynomials
Recall the following properties of exponents :
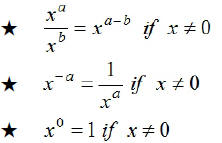
Simplify each of the following . Write without 0 or
negative exponents.
EX1.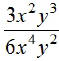
EX2.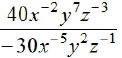
EX3.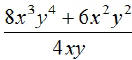
EX4.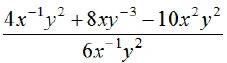
Use long division to find the quotient (and remainder)
when you divide
579 by 23.
The long division algorithm consists of 4 steps :
DIVIDE MULTIPLY SUBTRACT BRING DOWN
It is good practice to check your answers. Also, both the divisor and the
dividend should be arranged in descending order. If the dividend is
missing any intermediate powers of the variable , these powers should be
written with a coefficient of 0. [Note. This is a recommendation but not a
requirement.]
EX5.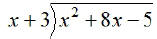
EX6.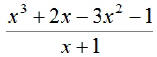
EX7.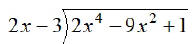
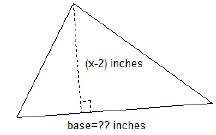
EX8. If the area of the triangle shown below is
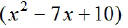square
inches, find an expression for its base.
EX9. If the area of the rectangle shown below is
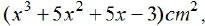find an expression representing its
perimeter.
