Table 1: Possible states of oil reserves.
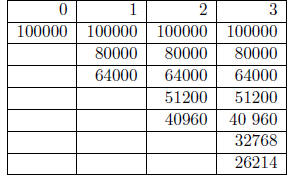
Table 2: Optimal pumping strategy.
| 0 |
1 |
2 |
| 366744 [Enhance] |
340364 [Enhance] |
240000 [Enhance] |
| |
226473 [Enhance] |
168000 [Enhance] |
| |
139418 [Enhance] |
110400 [Enhance] |
| |
|
64320 [Enhance] |
| |
|
31920 [Normal] |
Solution to Problem 1. The \trinomial lattice" that represents the
possible states of oil
reserves is given in Table 1. The value of the oil well at each sate and the
optimal pumping
strategy is given in Table 2. Consider, for example, the state of having 80000
barrels at time
t = 1. Let d = 1/1.1. The value at this state is the maximum of the three
choices
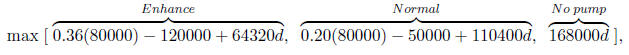
which is achieved by enhancing for a value of 226473.
Solution to Problem 2.
Part a. The Bellman equation for this problem is
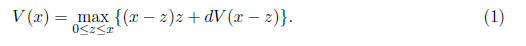
Part b. Suppose that V (x) = Kx for some K > 0. Then
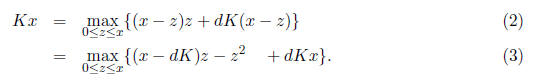
The optimal z(x) is found by taking the derivative of the quadratic function
of z inside the
braces and setting the resulting equation to zero . You can verify that
Substituting z (x) back into the quadratic function of z inside the braces,
and performing a bit
of algebra , we have
The right-hand side of (5) is a quadratic nonlinear function of x, whereas
the left-hand side
is a linear function of x. The two sides "do not match," and so the functional
form for the
optimal value function V (•) cannot be linear .
Part c. Here, one simply maximizes the quadratic function of z given by (x-z)z.
The optimal
solution is z(x) = x/2 and the objective function is (x - x/2)(x/2) = x^2/4.
Part d. The solution to part (c) suggests that V (x) = Kx^2 for some positive
K and that the
optimal policy is z(x) = Cx for some positive C. You can verify that if you set
V (x) = Kx^2
on the right-hand side of the Bellman equation, the right-hand side is still a
quadratic function
of z. The optimal value z(x) will be linear in x , and the optimal objective
function value will
remain quadratic upon substitution. The solution to Part (e) below will verify
this and provide
an exact solution.
Part e. Consider the right-hand side of the Bellman equation when V (x) = Kx^2.
Taking the
derivative of the function (x - z)z + dK(x - z)^2 with respect to z and setting
it to zero yields
0 = x - 2z- 2dK(x - z), and thus
Define
Given the value for K, we can express the optimal policy as
The optimal objective function value of the right-hand side of the Bellman
equation is therefore
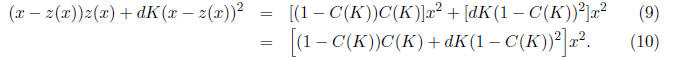
The right-hand side function must be identical to the left-hand side
function, which is, by
assumption, Kx^2. If our assumption is correct, then a value of K exists such
that
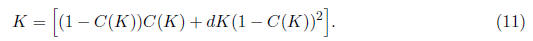
Assume d = 1/1.1. We can solve for the value of K and thus C(K) using
successive
approximations. That is, we can define
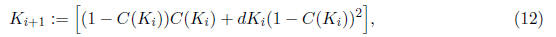
where C(Ki) is defined in (7). Assuming V0(•) = 0 is identical to setting K0 =
0. This yields
C(0) = 0.5 from (7). Substituting C(0) = 0.5 into the right-hand side of (11)
yields K1 = 0.25.
(We're just repeating the myopic solution so far.) The value of C(0.25) is
0.3529. Substituting
C(0.25) = 0.3529 into the right-hand side of (11) yields K2 = 0.3235. The value
of C(0.3235)
is 0.2917. Substituting C(0.3235) = 0.2917 into the right-hand side of (11)
yields K3 = 0.3402.
The process continues. The Ki converge to
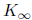:= 0.38416876 and C(
) =
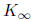0.231662479.
Remark. The identity (11) can be directly solved for K ,
but it requires a bit of lengthy algebra.
It turns out that the right-hand side simplifies to the reciprocal of 4(1 - dK).
Thus, the K
value we seek satisfies the identity 1 = 4(1-dK)K or 4dK^2 -4K +1 = 0. The
solution to this
quadratic equation is
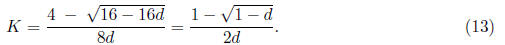
(The larger root will be larger than 1/2d, which will
yield a negative value for C(K).) Since
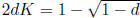it follows that
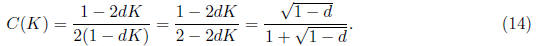
Note that C = 0.5 when d = 0, as it should.
