Your primary method for reviewing for the final should be to go over all assigned
homework problems.
If you cannot remember how to solve any of them, or are unsure, then you need to
work on those
problems.
Be sure to pay special attention to chapters 18-23, since those topics have not
appeared on either of the
midterms. They are more likely than other topics to appear on the final exam.
When using old final exams for study, keep in mind that chapter 10 is no longer
covered in this course,
yet many old finals contain problems based on chapter 10 concepts. You can
recognize a lot of these by
the presence of the sum or difference of multipart functions. You are not
responsible for knowing how
to solve these problems.
• Chapter 1, 2, 3, 4 - The Coordinate Plane, Lines and Circles
– You should understand the idea of imposing a coordinate system and the use of
the distance
formula.
– You should understand the various forms of the equations of a line , and be
able to determine
a line given either two points on the line, or the slope and a point on a line.
– You should understand the equation of a circle, and be able to find the
intersections of lines
with lines, and lines with circles. You should be able to do this in the context
of a model.
– You should be able to create a linear model for the relationship between two
quantities (e.g.,
population varying with time). If you have two such models, you should be able
to answer
various questions about the two quantities modeled (e.g., when are they equal?
when is one
twice as large as the other?)
– Especially good problems include 2.6, 2.13, 2.14, 3.4, 3.7, 4.8, 4.12, 4.14,
4.15.
• Chapters 5, 6 - Functions and Graphs
– You should know a function is. You should know what the domain, range and
graph of a
function are, and, if asked be able to find the domain and range of a particular
function. You
should know what the vertical line test is all about.
– You should be able to graph linear functions, and multipart functions whose
parts are linear.
– You should understand what a multipart function is. You should be able to
describe relationships
between two quantities with a multipart function, i.e., you should be able to
model
with them.
– Especially good problems include 5.10, 6.3, 6.4, 6.5, 6.6.
• Chapter 7 - Quadratic Functions
– You should know that quadratic functions are those of the form f(x) = ax2 +bx+c
and that
these can always be put into vertex form f(x) = a(x−h)2 +k. You should be able
to find the
vertex of a quadratic function.
– You should be able to create quadratic models given three generic points, or
the vertex and
one other point.
– You should be able to find the maximum or minimum value of a quantity
determined by a
quadratic function by considering the vertex.
– I like problems 7.10-7.14 a lot.
• Chapter 8 - Composition
– You should know what it means to compose two functions. You should understand
what
is meant by f(g(x)). You should know that f(g(x)) and g(f(x)) are generally
different functions .
You should be able towrite simplified rules for compositions f(g(x)) and g(f(x))
given
rules for f (x) and g(x).
– I particularly like problems 8.3, 8.4 and 8.5.
• Chapter 9 - Three Construction Tools
– You should understand horizontal and vertical shifting, and horizontal and
vertical scaling
(aka dilating)
– You should understand how to derive the graph of g(x) = af(bx + c) + d from
the graph of
f(x) (see, e.g., problem 9.2)
– I especially like problem 9.2, and 9.4.
• Chapter 11 - Inverse Functions
– A very short chapter.
– You should understand what an inverse function is, what conditions a function
must satisfy
in order to have an inverse (do all functions have inverses? can you tell if a
function has an
inverse by looking at its graph?), and how to find the inverse of a given
function
– You should understand what a one-to-one function is, and what is special about
the graph
of a one-to-one function
– I like problems 11.7 and 11.8.
• Chapter 12 - Rational Functions
– You should be able to model with linear-to-linear rational functions. This
comes down to
finding a rational function of the form
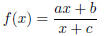
whose graph
1. passes through three given points
or
2. has a given asymptote and passes through two given points
or
3. has two given asymptotes and passes through one given point
You will need to translate the language of the modeling problem.
Pay particularly close attention to the words “linear-to-linear”.
Note that a linear-to-linear function is not a linear function.
– I especially like problems 12.1, 12.7, 12.8, 12.10, and 12.11.
• Chapter 13 - Measuring an Angle
– You should understand how to convert between degrees and radians
– You should understand and be able to use the relationships between radii,
angle, arc length
and area
– I like problems 13.8 and 13.9.
• Chapter 14 - Measuring Circular Motion
– You should understand the various measures of angular speed (aka angular
velocity), like
rpm, radians per second, or degrees per hour
– You should understand the relationship between radius, angular speed and
linear speed
– You should know how solve a belt-and-pulley problem (e.g., the bicycle example
from lecture,
example 14.4.1, problems 14.3, 14.9 and 14.11)
– I like problems 14.5 and 14.7.
• Chapter 15 - The Circular Functions
– This chapter introduces the trigonometric functions.
– You should be able to solve problems using the idea of trigonometric functions
as ratios of
sides of right triangles (e.g., problems 15.3, 15.4, 15.9, 15.10) and some
algebra
– You should understand the definitions of sin x and cos x using the unit
circle; you should be
able to determine certain simple properties of the functions sin x and cos x
from this definition
(e.g., the range, the domain, the graph, the values at certain value of x, like
x = 5π /2)
– You should be able to determine the location of an object moving circularly
given information
about its speed and starting location (e.g., problems 15.2, 15.5, 15.6, 15.11,
15.13)
• Chapter 16 - Trigonometric Functions
– This is a short chapter which adds some final touches to our knowledge of the
functions sin x
and cos x and related functions.
– I like problems 16.3 and 16.4
• Chapters 17, 18 - Sinusoidal Functions
– You should understand the notion of a sinusoidal function as a shifted/dilated
version of
the function sin x.
– You should understand the effect of the four parameters A,B,C and D on the
graph of
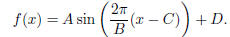
– You should be able to model with sinusoidal functions. In particular, you
should be able to
determine the parameters A,B,C, and D from a verbal description of a quantity
that varies
sinusoidally with time (see problems 17.2, 17.3, 17.4,17.6)
– You should be able to solve equations of the form f(x) = k where f is a
sinusoidal function;
if there are any solutions , there are infinitely many, and you should be able to
find them. You
should be able to do this in the context of a modeling problem (e.g., problems
18.2, 18.4, 18.6,
18.10, 18.11, 18.12)
• Chapters 19, 20, 21 - Exponential functions, modeling
and logartithms
– You should be able to recognize functions of the form f(x) = A0bx or,
equivalently, f(x) =
A0ekx. You should be able to put exponential functions into these forms.
– You should be able to create exponential models of quantities that change over
time. Given
two values of the quantity at two data points in time, you should be able to
come up with
an exponential model that fits the data. Given a single data point and
information about the
quantity’s rate of growth (e.g., percentage annual increase, or doubling time),
you should be
able to come up with an exponential model that fits.
– You should be able to solve equations involving exponential functions using
the natural logarithm.
– Relevant problems include 20.1,20.2, 21.9,21.11, 21.12, 21.15 and 21.16.
• Chapters 22, 23 - Parametric Equations and Uniform
Linear Motion
– You should understand what it means to describe motion using a pair of
parametric equations
x = f(t), y = g(t).
– You should know that uniform linear motion (i.e., constant speed motion along a
line) can be
described parametrically with two linear functions x(t) = a + bt, y(t) = c + dt.
– You should be able to model uniform linear motion using linear parametric
equations given
a variety of forms of description of the motion. For instance, knowing the
moving object’s
starting point, direction of motion and speed. Or, knowing the object’s location
at two different
points in time. See, e.g., problems 23.1, 23.2, 23.3, and 23.10.



