Recall
The Fundamental Theorem of Algebra If f(x) is
a polynomial of degree n with complex coefficients,
then f(x) has n complex roots. //
It is most often utilized in this alternate form:
FTAlg If f(x) is a polynomial of degree n with real
coefficients, then f(x) has at most n real roots. //
Notice that in both cases, we are considering
polynomials whose coefficients are drawn from a
field (either C or R). We have seen that Zp, the set
of congruence classes modulo a prime p, also forms
a field. So does the Fundamental Theorem of
Algebra hold in this setting?
Example: x^2 ≡ 1 (mod7). We have seen that this
congruence must have exactly two solutions , x ≡ ±1 (mod 7).
Example: x^2 ≡ −1 (mod7). By testing the
possibilities x ≡ 0,1,2,3,4,5,6 (mod7), we find that
this congruence has no solutions.
Example: x^2 +3x + 4 ≡ 0 (mod7). Even though we
are engaged in mod 7 arithmetic , rather than real
number arithmetic , we can still approach the
solution of this congruence by means of the
quadratic formula ,
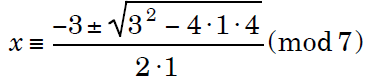
(provided we interpret the division in the formula
above as multiplication by the inverse mod 7 of 2),
or what is the same, the values of x that solve the
original congruence are solutions to the linear
congruence
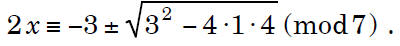
Of course, there is still the significant matter of
what it means to compute a square root mod 7.
Note that since the discriminant
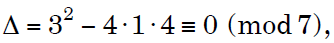
our original congruence has only one solution,
corresponding to the solution of the linear
congruence 2 *1x + 3 ≡ 0 (mod7). That is, x ≡ 2 (mod 7).
Lagrange’s Theorem If f(x) is a polynomial of
degree n with integer coefficients so that at least
one coefficient is not divisible by the prime p, then
f (x) ≡ 0 (mod p) has at most n roots modulo p.
Proof By Strong Induction on n:
Base case: When n = 1, we have a linear
congruence of the form ax ≡ b (mod p). So either
(a, p) = 1 and there is one solution to the
congruence, or (a, p) = p, whence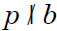 
, and there
are no solutions mod p.
Induction step : Assume that the theorem holds for
polynomials of degree less than some fixed n;
suppose that f(x) is a polynomial of degree exactly
n. If f(x) has no roots mod p, then the theorem
holds, so we can assume that there is at least one
root : x ≡ a (mod p). Division of f(x) by x – a
produces a quotient polynomial q(x) and a
remainder, which must have degree smaller than 1,
hence is itself an integer r. That is,
f(x) = (x − a) *q(x) + r . But since
f (a) ≡ 0 (mod p), we
must have that r ≡ 0 (mod p). Therefore,
f (x) ≡ (x − a) *q(x) (mod p). Now if
x ≡ b (mod p) is a different root of f(x), then
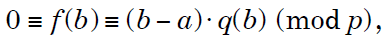
and since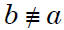 
(mod p) , we
can cancel the factor
(b – a) above, proving that b is a root of q(x) as well.
However, q(x) has degree less than n and has at
least one coefficient not divisible by p (else all the
coefficients of f(x) are divisible by p), so the
induction hypothesis applies to q(x), allowing us to
conclude that q(x) has at most n – 1 distinct roots
mod p. Therefore, f (x) ≡ 0 (mod p) has at most n
distinct roots modulo p. //
It is important to recognize that Lagrange’s
Theorem applies only to congruences with prime
moduli.
Example: x^2 ≡ 1 (mod 8) has four solutions x ≡
1,3,5,7 (mod 8).
Corollary Suppose p is a prime and n|p −1. Then
x^n ≡ 1 (mod p) has exactly n solutions mod p.
Proof Recall that if p – 1 = mn,
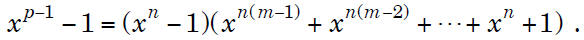
Now Lagrange’s Theorem says that the two
polynomial factors on the right have at most n and
at most n(m−1) roots mod p, respectively — a total
of at most n + n(m−1) = p −1 roots. But Fermat’s
Little Theorem says that the polynomial on the left
has exactly p – 1 roots mod p. Therefore both
factors on the right must have the maximum
number of roots possible. In particular, x^n −1 has
exactly n roots mod p. //
