Problems.
In problems asking for numerical or symbolic answer, you have to prove (same as
‘explain’, same
as ‘justify’) your method . Sometimes we remind about this in the problem’s
statement, sometimes
we do not. Often you can just refer to the main facts proved in this handout.
The statement of the
form ‘If A, then B’ means the same as ‘Given A, prove B’. Proof of the statement
of the form ‘A if
and only if B’ usually amounts to two proofs : ‘If A, then B’ and ‘If B, then A’.
1. For each of the following quadratic polynomials (a) complete the square; (b)
find the minimum or
the maximum values of the corresponding functions and the value of x for which
it is attained;
(c) find the roots (i.e. solve the corresponding quadratic equation); (d) sketch
the corresponding
parabola.
(i) x2
(ii) x2 + 6x + 9
(iii) x2 + 6x
(iv) −2x2 − 5
(v) −2x2 + 5
(vi) x2 − 2x + 3
(vii) 3x2 + 4x − 1
(viii) −2x2 + 4x − 1
2. Prove that a quadratic function f(x) = ax2 + bx + c, with a > 0 (a < 0),
(with the domain R -
the set of all real numbers ) always attains the minimum (maximum) value exactly
for one value of
x, and does not attain maximum (minimum) value.
What is this value of x?
3. (i) Among all pairs of two real numbers whose sum is 10, find the pair with
the greatest product.
Justify. What is the maximum value of the product ? What can be said about the
minimum value
of the product?
Generalize, by replacing 10 with an arbitrary positive number s.
(ii) Among all rectangles with perimeter 20 find the one of the greatest area.
What is the maximum
area?
Generalize, by replacing 20 with an arbitrary positive number p.
4. Find all pairs of real numbers (x, y) such that x2 + y2 + 6x = 10y − 34.
5. Let x1 and x2 be the roots of the quadratic polynomial f(x) = 5x2 − 20x − 1.
Compute
(i) 2(x1 + x2)
(ii) (x1x2)3
(iii)
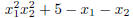
(iv) 1/x1 + 1/x2
(v)
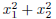
(vi)
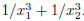
6. Factor the following quadratic polynomials into the product of the first
degree polynomials with
real coefficients and with the coefficients at x equal to 1, or show that no
such factorization exists.
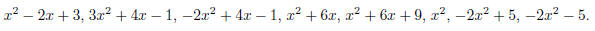
7. Find the coordinates of the points of intersections (or show that they do not
exist) of the line
y = 2x + 1 and the following parabolas. You do not have to draw graphs to solve
this problem,
but it is instructive to draw them after the solution is obtained in order to
see what happens
”geometrically”.
(i) y = x2 + 4x − 3
(ii) y = x2 + 4x + 10
(iii) y = x2 + 4x + 2
8. Prove that a parabola and a line can intersect only at 0, or 1, or 2 points.
(Often, when a parabola and a nonvertical line intersect at 1 point, we say that
they intersect at
two equal points, or that the line is tangent to the parabola.)
9. Find an equation of a parabola (or show that no parabola exist) which passes
through the points
(i) (1, 1), (−2, 0) and (3, 5)
(ii) (1, 1), (1,−10) and (3, 5)
(iii) (0, 3), and has its vertex at (−2,−7);
(iv) (2, 5), (−1, 7), and has its vertex at (1, 4).
—————————————————————-
10. For which values of r, the equation x2 + 4rx + (5 + 4r) = 0 has
(i) two distinct real roots?
(ii) two equal real roots?
11. For which values of r, the equation x2 + (4 + 2r)x + (5 + 4r) = 0 has
(i) equal roots?
(ii) opposite roots? (i.e., with equal absolute values, but
different signs .)
12. Prove that for every three non-collinear points (x1, y1), (x2, y2), (x3,
y3), (i.e., the points are
not on a line) and with pairwise distinct x-coordinates, there exists exactly
one parabola passing
through them.
Will the conclusion hold if we allow the three points to be collinear? Will the
conclusion hold if we
allow two of the points lie on a vertical line?
13. For which values of a, the line y = 3x + a and the parabola y = x2 + x have
(i) two common
points? (ii) one common point ? (iii) no common points?
14. Prove that the graph of the parabola y = f(x) = ax2 + bx + c is symmetric
with respect to the
vertical line x = −b/2a.
The line x = −b/2a is called the axis of the parabola.
(Hint: First realize that it amounts showing that the points of the graph whose
x-coordinates are
symmetric with respect to the number −b/2a have equal y-coordinates.
Symbolically this means that
for every number h, f(−b/2a − h) = f(−b/2a + h). Therefore we have to check the
latter.)
15. Prove that for all real numbers x, y, the polynomial x 2 +xy +y2
≥ 0 and that
it takes value zero
if and only if x = y = 0.
16. (i) If 2a + 3b = 12, what is the greatest value of ab? Justify.
(ii) If ab = 12, what is the smallest value of a2 + b2? Justify.
—————————————————————————————————————————-
17. Find all value of a for which the polynomials x2+ax+1 and x2+x+a have at
least one common
(real) root.
18. Prove that for all real numbers x, y, z, x2 + y2 + z2
≥ xy + yz + zx and the
equality sign is
attained if and only if x = y = z.
19. Prove that for all real numbers x, y, z, x + y + z = 1 implies that x2
+ y2
+ z2 ≥ 1/3, and the
equality sign is attained if and only if x = y = z.
20. Prove that for all real numbers x, y, z, x + y + z ≥ 0 implies x3 + y3 + z3
≥ 3xyz. Then show
that x3 + y3 + z3 = 3xyz if and only if x = y = z or x + y + z = 0.
21. Among all rectangles with area a > 0, find the one of the smallest perimeter
(i.e., determine the
lengths of its sides).
22. A stone moves in such a way that its height after t seconds of its motion is
given by the formula
h(t) = −16t2 +96t+256 feet. How high will the stone go? At what moment(s) of
time will it be
144 feet high? When does it hit the ground?
*********************************************************************************



