Precalculus

B.1: The Cartesian Plane

Distance Formula :
The Distance between two points 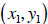and 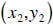is given by

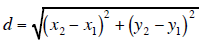
Midpoint Formula:
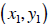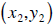The Midpoint between two points and is given by

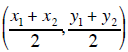
Equation of a Circle:
The equation of a circle with Radius r and Center (h,k) is given by

r² = (x - h)²+ (y- k)²

B.3: Solving Equations Algebraically and Graphically

Extraneous Solutions:
A solution that arrives while solving for a variable that, when plugged
back into the original equation, does not make equality hold.

In other words: CHECK YOUR SOLUTIONS!!!

X-Intercepts:
An x-intercept occurs where y=0 or the function =0.

Y-Intercepts:
A y-intercept occurs where x=0.
Graphical Interpretation of a Real Solution:
Where the graph intersects the x-axis; x-intercepts

Solving a Quadratic by Factoring :
1.) Get everything on one side and 0 on the other side.
2.) Factor.
3.) Set each Factor equal to 0.
4.) CHECK your answers.

Solving a Quadratic by extracting square roots :
1.) If the Quadratic is in the form (ax + b)² = c , write
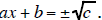
2.) Solve 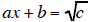and
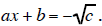
3.) CHECK your answers.

Solving a Quadratic by Completing the Square:
Before you begin, write your equation in the form ax² + bx = c .
1.) Take the square root of the first term .
2.) Take the middle term divided by your answer from the Step 1.
3.) Take the answer from Step 2 and divide it by 2.
4.) Take the answer from Step 3 and square it.
5.) Add the answer from Step 4 to each side of the equation.
6.) Factor the left and simplify the right
NOTE: The left always factors as  (#1+# 3)² .
7.) Use the Extracting square roots method to solve .
8.) CHECK your answers.

Solving a Quadratic using the Quadratic Formula:
1.) Write your equation in the form ax² + bx + c = 0.
2.) Use the Quadratc formula: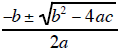
3.) CHECK your answers.

B.4: Solving Inequalities Algebraically and Graphically

Remember:
If you multiply or divide both sides of an inequality by a negative
number, you MUST switch the inequality sign .

Absolute Value Inequalities :
When given
|something|  < a, this becomes two problems :
something < a and something > -a

Likewise , when given |something| > a, this becomes two problems:
something > a andsomething < -a

Example:

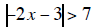
This becomes two problems:
-2x -3 > 7 and -2x - 3 <-7.

We can then solve each of these separately to get
x < -5 and x > 2. (Check to see if you get the same thing.)

Polynomial Inequalities :
1.) Get everything one one side and 0 on the other side.
2.) Factor.
3.) Set each factor equal to 0. The answers you get are your
CRITICAL VALUES.
4.) Set up test intervals using your Critical values to divide the
number line.
5.) Plug in test values to determine if each interval is positive or
negative .
6.) Choose the appropriate intervals for your original problem.

Rational Inequalities :
1.) Get everything one one side and 0 on the other side.
2.) Rewrite the non- zero side as a single fraction.
3.) Factor the top AND bottom of the fraction.
4.) Set each factor equal to 0. The answers you get are your
CRITICAL VALUES.
5.) Set up test intervals using your Critical values to divide the
number line.
6.) Plug in test values to determine if each interval is positive or
negative.
7.) Choose the appropriate intervals for your original problem.