1. Let p = 101010 · · · 01 be the m- digit number in which
the first and last digits are 1 and the
digits alternate between 1 and 0. For which positive integers m is the number p
prime.
SOLUTION. First, the number m of digits must be odd
since both the first and last digit of
p is 1. Next, 11p = 10p + p is the number 111 · · · 1 with m + 1 digits all
equal to 1. Thus
11p = (10m+1 −1)/9, and we have 99p = 10m+1 −1. Since m+1 is even, we can write
m+1 = 2a
with a ≥ 1, and we obtain 99p = 102a−1 = (10a−1)(10a+1). If p is prime, then p
must divide one
of the factors 10a−1 or 10a+1, and in either case, we get p ≤ 10a+1. Since 99p =
(10a−1)(10a+1),
we deduce that 99 ≥ 10a − 1. But 99 = 102 − 1, so we see that a
≤ 2. If a = 2,
then m = 3 and
p = 101 is indeed a prime number. The only other possibility is a = 1, in which
case m = 1 and
p = 1. Since the number 1 is not prime , by definition, the only solution is m =
3.
2. In the figure on the right, hexagon ABCDEF is divided
into three squares and four triangles.
Show that the areas of all four triangles are equal.
SOLUTION. Let X, Y and Z be the third vertices of the
triangles
with side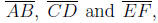 
respectively. We will prove
that the area of
ΔABX
is equal to the area of ΔXY Z. Similar
arguments show that the areas of ΔCDY and ΔEFZ also equal
the area of ΔXY Z, and thus all four triangles have equal areas.
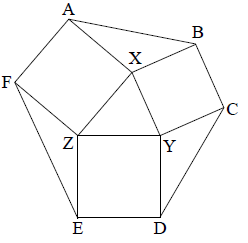
Imagine rotating ΔXY Z about vertex X so as to make
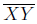
coincide with
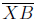. This is possible since
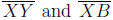are two
sides of a square, and hence have equal lengths. Also note that this
is a rotation through 90° and that ∠AXZ = 90°. In particular, if
Z' is the new position of point Z, then ∠AXZ' = 180°. In other
words, points A, X and Z' lie on a line , and we see that
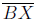is a
median of ΔAZB, since AX = XZ = XZ'.
Now, a median of a triangle always divides the triangle
into two triangles with equal area, and
thus the areas of ΔABX and of ΔXBZ' are equal. The latter triangle, however, is
just a rotation
of ΔXY Z and so its area is equal to that of ΔXY Z. It follows that ΔABX and ΔXY
Z have
equal areas, as wanted.
3. Find all positive integers x and y such that x ≤ y ≤ 2x
and 1 + x2 + y2 = 3xy.
SOLUTION. Since x ≤ y ≤ 2x, we see y is at most
distance x/2 from 3x/2, or equivalently that
|y−3x/2| ≤ x/2. Squaring the latter yields y2−3xy+9x2/4 ≤ x2/4, and thus
y2−3xy+2x2 ≤ 0.
But y2 − 3xy + 2x2 = x2 + (y2 − 3xy + x2) = x2 − 1, so the previous inequality
yields x2 − 1 ≤ 0
and, since x is a positive integer, we conclude that x = 1. Furthermore, since 1
= x ≤ y ≤ 2x = 2,
we see that y = 1 or 2 are the only possibilities. Finally, we note that the
pairs x = 1, y = 1
and x = 1, y = 2 both satisfy the equation 1 + x2 + y2 = 3xy and consequently we
have found all
solutions to the given equation and inequalities .
4. Your calculator will show that the number
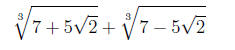
is approximately an integer. Decide whether or not it is
exactly an integer, and prove that
your answer is correct.
SOLUTION. Let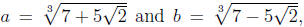 
and write
s = a + b. Our task is to
determine whether or not s is an integer. Observe that
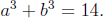Also, ab is the cube root of
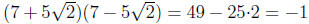and thus ab = −1. Since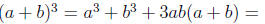
14 − 3(a + b), it follows that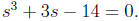 
Your calculator says that s is approximately 2, so we
might guess that s = 2, and we check
that 2 really is a solution of the cubic equation s3+3s−14 = 0. This does not
complete the proof,
however, because we must consider the possibility that our cubic equation also
has other roots
near 2. Since s = 2 is a root, we see that (s−2) must be a factor of s 3 +3s−14,
and we calculate
by long division that s3 + 3s − 14 = (s − 2)(s2 + 2s + 7). Thus if s is not 2,
then s2 + 2s + 7 = 0.
But this quadratic equation has no real root, so the only possibility is s = 2,
which, of course, is
an integer.
5. Let Fn be the nth Fibonacci number. Thus F1 = 1, F2 =
1, F3 = 2, F4 = 3, F5 = 5,
and in general for n > 2, we have Fn = Fn-1 + Fn-2. Now for each integer n
≥ 1,
write
An = (Fn+1)2 − (Fn)2 − FnFn+1 and Bn = (Fn)2 + (Fn+2)2 − 3FnFn+2. Find simple
formulas
for An and Bn and use them to compute A1000 and B1000.
SOLUTION. Let n > 1 and use the fact that Fn+1 = Fn + Fn-1
to compute that
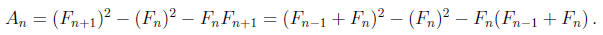
Simplifying this , we get An = (Fn-1)2+Fn-1Fn−(Fn)2, and
this is exactly −An-1. Since A1 = −1,
we deduce that A2 = 1, A3 = −1 and in general An = (−1)n. Thus A1000 = 1.
Also
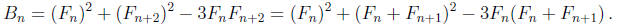
Simplifying this, we get Bn = −(Fn)2 − FnFn+1 + (Fn+1)2,
and so Bn = An. In particular,
Bn = (−1)n and B1000 = 1.
If n is odd and we write x = Fn and y = Fn+2 then we have
−1 = Bn = x2 + y2 − 3xy. Thus
x and y satisfy the equation 1 + x2 + y2 = 3xy of Problem 3, and we conclude
that this equation
has infinitely many pairs of positive integer solutions.
