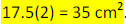Midpoint

Intro

If you measure a line segment that is 10 inches long and divide it into two 5-inch segments, you
get two equal halves. The point at which you divide the line is called the midpoint.

The midpoint of a line segment divides the segment into two congruent parts.

Finding the midpoint of a line segment on a coordinate system is quite simple if the line is
either horizontal or vertical; simply measure the length of the segment and divide by two. For
example,

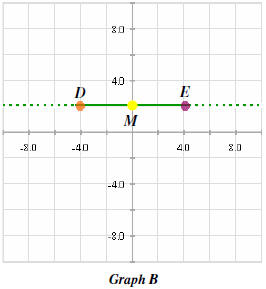
In this example, the length of the vertical segment, AB, is 5 units. Therefore, the midpoint of AB is 2.5 units from either point.	In this example, the length of the vertical segment, DE, is 4 units. Therefore, the midpoint of DE is 2 units from either point.
Namely, the point M(-4 , -3.5).	Namely, the point M(0 , 1).

However, the process becomes a bit more challenging when trying to find the midpoint of a
diagonal segment.

Midpoint Formula

Examining the two graphs more closely , we can determine how the midpoint is being calculated
each time. This will help us in finding a general formula we can use for each scenario .

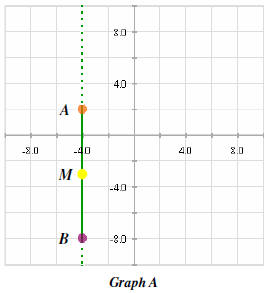
Graph A shows a line segment, AB, whose coordinates are A (-4,1) and B(-4,-8); the midpoint of
AB is M(-4,-3).

If we think about the general concept of midpoint it is really finding the middle -point or
average of two numbers . Following this thought process, we can see if finding the average of
the x- values and the average of the y-values yields the midpoint:

Midpoint of AB

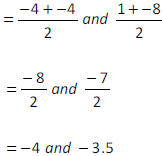
From this calculation , I can see finding the average of the x- values and y -values do indeed yield
the midpoint. Try the same process with the information in graph B.

The midpoint of a segment with endpoints ( x₁, y₁ ) ( x₂, y₂ ) is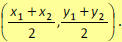

Applications using the Midpoint Formula

Example 1

Find the coordinates of the center of the rectangle.

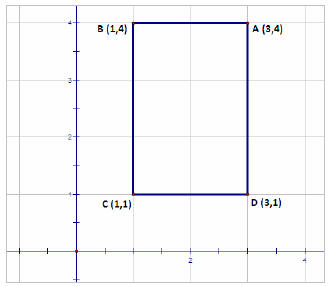
Solution
You can find the center of any rectangle by finding
the midpoint of either diagonal.

Using the diagonal AC:

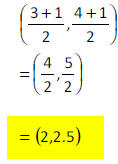
Example 2

Find the midpoint of the hypotenuse for the
right triangle, ΔBCD.

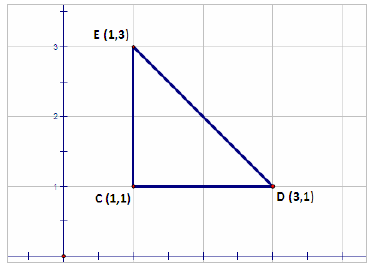
Solution
The hypotenuse of a right triangle is always
the side opposite the right angle; therefore,
the hypotenuse of ΔBCD is BD.

Using BD:

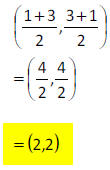
Example 3

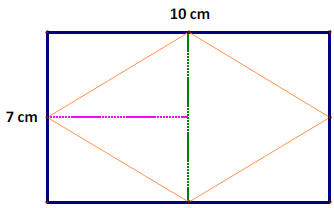
A rectangle is 10 cm long and 7 cm wide. What is
the area of the rhombus formed by connecting
the midpoints of each side of the rectangle?

Solution

A rhombus is comprised of two triangles . Draw a
line which connects the midpoints of the lengths
of the rectangle (in green).

Next, we can draw a height for the triangles (in pink). The height of the triangle must be 5cm
since the base connects the midpoints of the length of the rectangle.

Using our formula for finding the area of a triangle, 1/2bh, we can substitute our values :

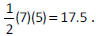
Finally, since there are two triangles, we can double the area: