Math 102 Study Guide - A Summary of Factoring
The intent of this document is not to teach you individual
techniques of factoring: the intent is to
summarize all of the techniques we have, and help you to recognize what the
appropriate steps to take are
on a given factoring problem .
I chose to organize this more or less in outline form. I think it’s helpful to
think of it as a flowchart.
I. Is there a common factor ?
The very beginning of EVERY factoring problem is looking for any common factors
that can be factored out.
Things to keep in mind:
• If you miss common factors that can be taken out, at best you make the problem
harder. At
worst, it’s essentially impossible.
• You can’t just divide by the common factor and forget about it! This
changes the problem. You
have to factor out the common factor, which means you write it multiplied
by whatever is left when you
divide it out.
• After you factor out the common stuff, take a look at the stuff left over and
decide whether you’re
done, or whether the stuff left over can be factored further using one of our
other techniques.
II. Are there two terms left to factor?
If, after either factoring out the common stuff, or deciding that there is no
common factor, you’re looking at
two terms , there are exactly three possibilities:
• If the expression has a DIFFERENCE of two things that
are squares, like x2 , 16, 25 y2 , x4...,
you’re looking at using the difference of squares formula :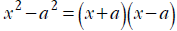
.IMPORTANT:
If your
expression is the SUM of two squares, it can’t be factored.
• If the expression is the difference of two cubes , like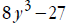
,use
the difference of cubes
formula: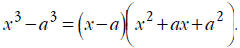
• If the expression is the sum of two cubes, like
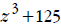(which is
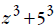)use
the sum of cubes
formula: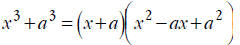
If you have any two-term expression with no common factor
that’s NOT one of these three possibilities, then
it does not factor.
III. Are there three terms left to factor?
This is the possibility that you probably spent the most time practicing in Math
101, and we’ll use it a lot in
here. It’s what I call “reverse FOIL”, because it is literally the opposite of
multiplying out parentheses using
FOIL .
IV. Are there four terms left to factor?
We only know of one way to factor four-term expressions with no common factor:
factoring by grouping.
In this case, what we do is group together the first two terms (using
parentheses), and the last two terms,
and see if there’s anything that can be factored out of
each of these sets of parentheses separately. If there
is, with any luck the stuff left over will be a common factor, just like the
example below.
Example:
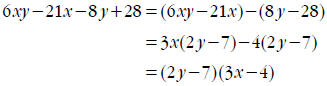
Notice that when we inserted parentheses in the second
step, we had to change the sign of the 28: this is
because when you insert the parentheses, this now means that you’re supposed to
distribute the negative
sign, which would change the sign of the 28. To account for that, we make it
negative so that distributing
out the parentheses would put it back to where it was originally.
If you follow the guidelines laid out here, there will never be any doubt on HOW
you need to factor
something: it will just be a question of doing the procedures we’ve learned.
