The Factor Tree

2.2 Exponents and Roots

EXPONENTS
In mathematics, there are shorthand ways of writing things. Exponents are an example of a
shorthand way to write repeated multiplication. An exponent can also be referred to as a power
of the base. For example, 3×3×3×3×3 can be written as 3⁵ . (3 multiplied by itself 5 times.)
The number 3 is called the base and the number 5 is called the exponent. (3×3×3×3×3 is
considered to be the expanded form of a base raised to an exponent.)
Exponents are not only used with numbers. They can be used with the letters of mathematics,
called variables. For example, x • x • x • x can be written as x⁴ , where the variable, x, is the base
and the number 4 is the exponent. An important concept to understand when working with
numbers and variables occurs when a number is placed before a variable as in 5x. The operation
performed is multiplication. 5x is the same as 5 times x.
How do exponents affect negative numbers ? Look at the following examples of the exponents
written in expanded form.

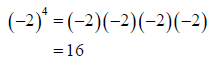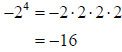When the negative is in the parentheses, the negative is included in the repeated multiplication.	When the negative is not in the parentheses, the negative is not included in the repeated multiplication. It is written once in the front.

Numbers and variables with no exponents showing are understood to have an exponent of 1. In
the example, 3x² , the 3 has an exponent of 1 and the x has an exponent of 2, allowing us to write
it in expanded form as 3• x • x .

The most common error that occurs when working with examples such as the one above is to
forget the fact that if an exponent is not showing it is understood to be a 1. This error causes
some to attach the exponent on the variable to both the number and the variable. In our example,
3x² , this error is seen when the 3 is written twice and the variable is written twice. The proper
way to write 3x² in expanded form is 3• x • x not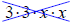. Recall, numbers and variables with
no exponent showing are understood to have an exponent of 1.

Example 1 Rewrite 4•4•4 with an exponent.
4³
4 multiplied by itself 3 times.

Example 2 Rewrite (-5)(-5)(-5)(-5)(-5)(-5) with an exponent.
(-5 )⁶ 
–5 multiplied by itself 6 times. The negative must be
enclosed in the parentheses because it is included in
the repeated multiplication.

Example 3 Rewrite -3•3• x • x • x • x with an exponent.
-3² x⁴
The negative is not enclosed in the parentheses
because it is not included in the repeated
multiplication.

Example 4 Rewrite 11 with an exponent.
11¹
A number and/or a variable written only once has an
exponent of 1.

Example 5 Rewrite 6² in expanded form.
6•6
6 multiplied by itself 2 times.

Example 6 Rewrite (-7)⁴  in expanded form.
(-7)(-7)(-7)(-7)
–7 multiplied by itself 4 times. Notice the negative
must be used in the repeated multiplication.

Example 7 Rewrite 8a³ in expanded form.
8• a • a • a
8 times “a” multiplied by itself 3 times.

Example 8 Rewrite −2³ x⁵ in expanded form.
−2• 2• 2• x • x • x • x • x
The negative is not used in the repeated
multiplication.

Example 9 Rewrite 9¹ in expanded form.
9
9 written 1 time.
An important rule for exponents to memorize is:
A base raised to the power of 0 will always equal 1.
(This rule will be discussed in more detail in chapter 9. For now, memorize it!)
For example:

Example 10 Find the value of 4³ .

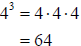
4 multiplied by itself 3 times.

Example 11 Find the value of 3⁰ .
3⁰ =1
A base raised to the power of 0 will always equal 1.

Example 12 Find the value of 12¹ .
12¹ =12
12 written 1 time.

Example 13 Rewrite −3⁴ in expanded form.

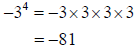
The negative is not used in the repeated
multiplication.

ROOTS OR RADICALS
Finding a root of a number is the opposite operation of raising a number to a power or exponent.
To learn the basics we will deal with roots of positive numbers only.
We will begin by looking at the notation used for roots.

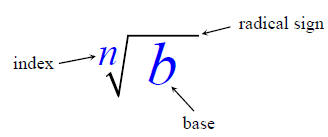
radical sign ()– tells us to find a root.
index (n) – tells us which root we are finding.
base (b) – the number to use to create a factor tree.

Note: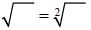 (If there is no index, it is the same as having an index of 2. This type of a
root is known as a square root .)

To find a root, start by prime factoring the base . Look for groups of the same number. (The size
of your group will depend on the index in your problem.) Once you have located a group of the
same number, place that number on the outside of the radical. Study the following examples.

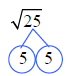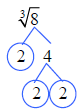
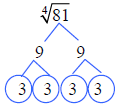
There is no index, so we know we are looking for a square root or group of two . There are two 5’s. The square root of 25 is 5.	The index is a three. We are looking for groups of three. There are three 2’s. the cube root of 8 is 2.	The index is four. We are looking for groups of four. There are four 3’s. The fourth root of 81 is 3.

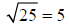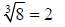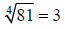Example 14 Find the indicated root.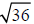

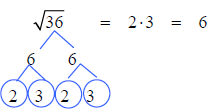
We are looking for groups of two.
There are two 2’s and two 3’s. The
square root will be the product of 2
and 3, which is 6.

This problem can be done much quicker by identifying the two 6’s.

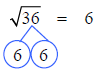
Identify a group of two.

Example 15 Find the indicated root.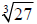

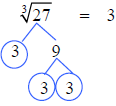
We are looking for groups of three.
There are three 3’s. The cube root of
27 is 3.

Example 16 Find the indicated root.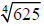

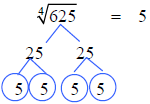
We are looking for groups of four.
There are four 5’s. The forth root of
625 is 5.

What happens when you don’t have equal groups? Study the following example.

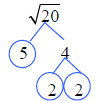
There is no index, so we are looking for groups of two. There is one group of 2’s, but we have a
5 left over that is not in a group. When this happens, whatever is left without a group must stay
under the radical sign.

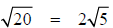
Example 17 Find the indicated root.

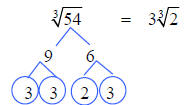
The index is 3, so we are looking for
groups of three. There are three 3’s
and one two. We place a 3 outside the
radical for the complete group. The 2
must stay under the radical.

Example 18 Find the indicated root.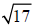

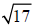
17 is a prime number. There will not be any groups.

Example 19 Find the indicated root.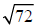

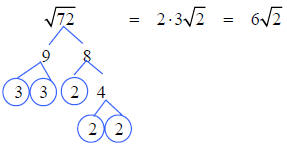
We are looking for groups of two.
There are two 3’s and three 2’s.
place one 2 and one 3 on the outside.
Leave one 2 inside the radical.

Example 20 Find the indicated root.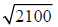

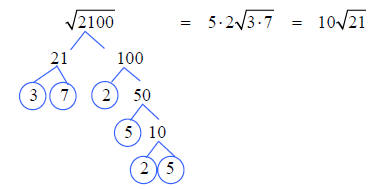
We are looking for groups of
two. There are two 3’s and three
2’s. Place one 2 and one 3 on
the outside. Leave one 2 inside
the radical.

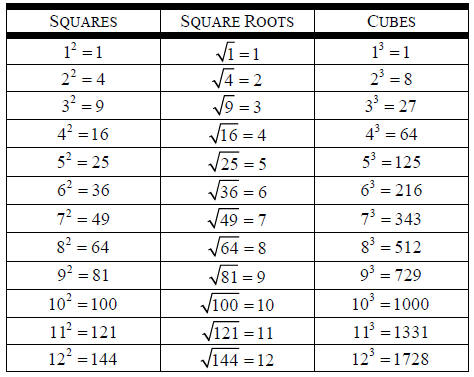
The following table of perfect squares and perfect cubes may help you with roots. This table is
also located in the Important Information Section of your book.

2.2 EXERCISES

Applications.
24. In 1990, Sanpete County ranked 1st in the United States in total population of turkeys
with more than 98 turkeys. What was the approximate turkey population of Sanpete
County?

25. A new fast food restaurant opened in a small town in Southern Utah. During its first
week of business the owner projected the number of customers to be served would be
153 . At the end of the first week the owner calculated that they actually served 84
customers. How many customers were served above the owners projected amount?