Introduction. Each group will analyze the
mathematical content of a given sample text. An Explanation
of how the analysis should be conducted is given below. Projects that are
insightful, clearly articulated, and
mathematically accurate will be awarded the most points.
Background. The Mathematics Learning Study Committee of the National
Research Council has put
forth a model of mathematical understanding called mathematical proficiency [1].
Mathematical proficiency
consists of the five following strands:
• conceptual understanding - comprehension of mathematical
concepts , operations , and relations
• procedural fluency - skill in carrying out procedures flexibly, accurately,
efficiently, and appropriately
• strategic competence - ability to formulate , represent, and solve mathematical
problems
• adaptive reasoning- capacity for logical thought , reflection, explanation, and
justification
• productive disposition - habitual inclination to see mathematics as sensible,
useful, and worthwhile,
coupled with a belief in diligence and one’s own efficacy.
You should keep in mind that these strands are
interdependent, and it is argued that for students to become
mathematical proficient , instructional programs must address each strand .
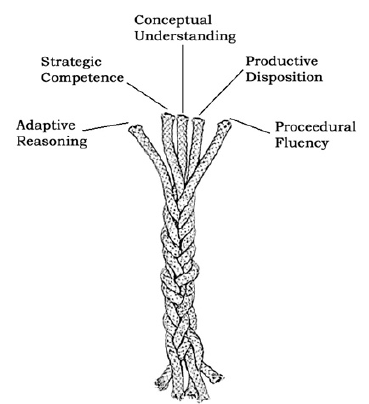
Figure 1. The intertwined strands of mathematical
proficiency.
Directions. Your project should consist of the
following in the form of a written or typed paper less than
two pages .
• A brief description of the mathematical concept(s) the
given investigation covers. In other words,
what should your students get from this lesson in a nutshell.
• Determine which of the five strands of mathematical
proficiency, given above, are covered in your
sample lesson. Give an explicit example of the content for each strand that you
have determined to
be in the lesson.
• If you find that some strands were not covered in the
lesson, then modify the sample lesson so that
it incorporates the missing strands.
Schedule.